Question

Which of the following correctly describes the variation of the speed $v$ and acceleration $a$ of a point mass falling vertically in a viscous medium that applies a force $F=-kv$, where k is a constant, on the body? (The graphs are schematic and are not drawn to scale)
A.

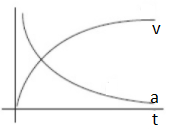
B.

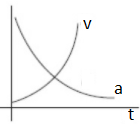
C.

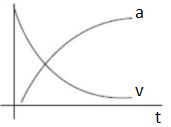
D.

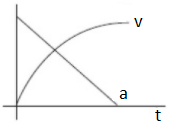
Answer 1

Hint: When a body(point mass) is free-falling from a defined distance from the surface of the earth the acceleration of the body is the same as the acceleration due to gravity acting on the point mass. The velocity of the body acts in the opposite direction of the motion of the body. By balancing the forces the equations for the values of acceleration and velocity can be easily obtained.

Complete step by step answer:
When we refer to the free body diagram of a free-falling body as shown in the diagram

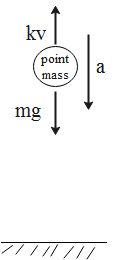
We get a balanced equation for forces as,
$ma=mg-kv\quad. ....(1)$
So when there is maximum acceleration ($a$), the velocity ($v$) of the body will be the least (zero).
So, the maximum velocity ${{v}_{\max }}$ of point mass will be,
$\begin{align}
  & mg-k{{v}_{\max }}=0 \\
 & \Rightarrow {{v}_{\max }}=\dfrac{mg}{k}\quad. ....(2) \\
\end{align}$
By reconsidering equation (1);
Diving both the sides by mass ($m$)
$a=g-\dfrac{kv}{m}$
we can simplify the equation as,
$\dfrac{dv}{dt}=g-\alpha v$
Where, $\alpha $ is an assumed constant equivalent to $\dfrac{k}{m}$
$dt=\dfrac{dv}{g-\alpha v}$
Integrating both the side in a definite range,
$\begin{align}
  & \int_{0}^{t}{dt}=\int_{0}^{v}{\dfrac{dv}{g-\alpha v}} \\
 & \Rightarrow t=-\dfrac{1}{\alpha }\ln \left[ g-\alpha v \right]_{0}^{v} \\
 & \Rightarrow -\alpha t=\ln \left( \dfrac{g-\alpha v}{g} \right) \\
 & \Rightarrow {{e}^{-\alpha t}}=\dfrac{g-\alpha v}{g} \\
\end{align}$
By putting the value of $\alpha $
\[\begin{align}
  & {{e}^{-\dfrac{k}{m}t}}=1-\dfrac{k}{mg}v \\
 & \Rightarrow {{e}^{-\dfrac{k}{m}t}}=1-\dfrac{v}{{{v}_{\max }}} \\
\end{align}\]
So by rearranging the equation of velocity ($v$) will be,
$v={{v}_{\max }}(1-{{e}^{-\alpha t}})\quad. ........(3)$
From this equation, we can conclude that the velocity of the object will be increasing exponentially.
The graphical representation of the acceleration and velocity concerning the increasing time is shown with the plot in option D.
Thus the correct option for the question is Option D.

Note: Acceleration of the body is the rate of change of velocity. We can easily plot the equations which are derived for the analysis of the motion of the body. When a body is in motion the forces acting on the body which accelerates the body is balanced by other forces acting on the body.