Question

Which number lies between \[\dfrac{{25}}{4}\] and \[\dfrac{{22}}{3}\]?

Answer 1

Hint:A number is an arithmetic value used for representing the quantity and used in making calculations. If a number is expressed in the form of p/q then it is a rational number. Here p and q are integers, and q is not equal to \[0\]. A rational number should have a numerator and denominator.

Complete step by step answer:
Let's discuss some points regarding numbers before solving this question. We are using numbers in our day-to-day life, such as counting money, time, things, and so on. We have different types of numbers in the number system. We will just have brief information about different types of numbers.
(a) Natural numbers - eg: N =\[\{ 1,2,3,...\} \]
(b) Whole numbers – eg: W =\[\{ 0,1,2,3,...\} \]
(c) Integers – eg: Z = \[\{ .... - 3, - 2,1,0,1,2,3,...\} \]
(d) Real numbers – eg: \[\{ - 10,0,\dfrac{3}{2},0.444,20,\sqrt {23,} ...\} \]
(e) Rational numbers – eg: \[\{ \dfrac{5}{9},\dfrac{4}{3},\dfrac{3}{1},\dfrac{0}{1},.....\} \]
(f) Irrational numbers – eg: \[\{ \sqrt 3 ,\pi ,....\} \]
(g) Complex numbers – eg: \[\{ 5 + 5i, - 2 + 3i,1 - \sqrt 3 i,....\} \]
(h) Imaginary numbers – eg: \[\{ {i^2},\sqrt 3 ,3i....\} \]

As we have discussed numbers, let’s solve this. Given numbers are as below,
\[\dfrac{{25}}{4}\] and \[\dfrac{{22}}{3}\]
Taking LCM of \[4\] and \[3\], which is \[12\]
\[\dfrac{{25}}{4} \times 3\] and \[\dfrac{{22}}{3} \times 4\]
\[\Rightarrow \dfrac{{75}}{{12}}\] and \[\dfrac{{88}}{{12}}\]
Thus, all the numbers that lie between\[\dfrac{{75}}{{12}}\] and \[\dfrac{{88}}{{12}}\] are as below:
\[\dfrac{{76}}{{12}},\dfrac{{77}}{{12}},\dfrac{{78}}{{12}},\dfrac{{79}}{{12}},\dfrac{{80}}{{12}},\dfrac{{81}}{{12}},\dfrac{{82}}{{12}},\dfrac{{83}}{{12}},\dfrac{{84}}{{12}},\dfrac{{85}}{{12}},\dfrac{{86}}{{12}},\dfrac{{87}}{{12}}\]

Also, if asked number of whole numbers that lie between them then,
\[\dfrac{{25}}{4} = 6.25\]
This means that this number lies between whole numbers \[6\] and \[7\].
\[\dfrac{{22}}{3} = 7.333...\]
This means that this number lies between whole numbers\[7\] and \[8\].

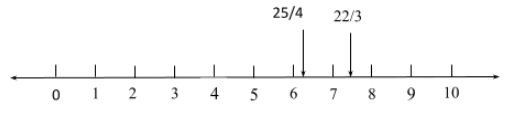
Hence, number \[7\] is the whole number that lies between \[\dfrac{{25}}{4}\] and \[\dfrac{{22}}{3}\].

Note:The whole numbers are defined as the positive integers including zero. The whole number does not contain any decimal or fractional part. It means that it represents the entire thing without pieces. A number line is a line on which numbers are marked at intervals. We will use the number line also to solve this given question.