Question

Which is the smallest of all the chords of a circle passing through a given point in it?
A. Chord trisected at the point.
B. Chord bisected at the point.
C. Chord passing through the center.
D. Both (A) and (B).

Answer 1

Hint: It is a theorem which we study in chapter “circles”. It states that out of all chords passing through a given point inside the circle, the smallest is one which is bisected at the point.

Complete step-by-step solution
Theorem: Out of all the chords passing through a given point in the circle, the smallest is one which is bisected at that point.
Proof: Let C (O, r) is a circle and let ‘N’ be a point inside the circle. O is the center and r is the radius of the circle.

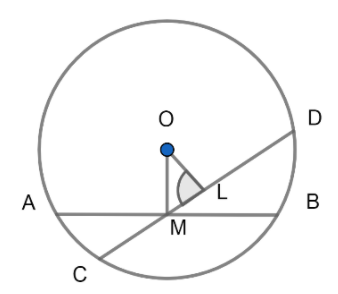
Let AB is the chord which is bisected by point M and CD is any other chord passing through M.
We have to prove that the smallest chord among all the chords which passes through M is AB.
So, we have to prove $AB< CD$ as AB is the chord which is passing through M and bisected at M and CD is any other chord passing through M.
So, let us prove $AB< CD$
For this first, join OM and draw OL perpendicular to CD as shown in the diagram above.
Now, in the right-angled triangle OLM, OM is the hypotenuse and we know that in a right-angled triangle, the hypotenuse is longer than both of the remaining sides.
$\Rightarrow OM> OL$
$\Rightarrow $ Chord CD is nearer to the center as compared to chord AB.
We know that in a circle the chord which is nearer to the circle is longer than the chord which is further from the center.
So, chord CD will be greater than chord AB in length
i.e. $CD> AB$
Thus, we have proved that $AB< CD$ i.e. AB is the smallest of all the chords passing through’ in the circle and so option (B) is the correct answer.

Note: In the solution, we have used a theorem “ Of any two chords of a circle, one which is nearer to the circle is greater in length”, we can prove this theorem as follows;

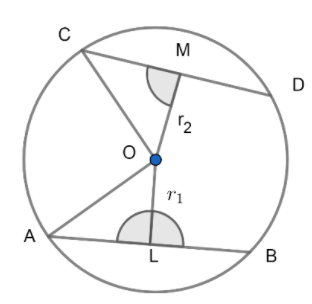
Let C (O,r) be a circle;
Given two chords AB and CD with distance ${{r}_{1}}\ and\ {{r}_{2}}$ from the centre respectively such that ${{r}_{1}}<{{r}_{2}}$
To prove: $AB>CD$
Proof: First join OA and OC.
We know that the perpendicular from the center bisects the chord.
So, $AL=\dfrac{1}{2}\left( AB \right)\ and\ CM=\dfrac{1}{2}\left( CD \right)$
In right triangle ALO;
${{\left( AL \right)}^{2}}+{{\left( LO \right)}^{2}}=O{{A}^{2}}$
${{\left( \dfrac{AB}{2} \right)}^{2}}+{{\left( {{r}_{1}} \right)}^{2}}={{r}^{2}}.........\left( 1 \right)$ (OA = r = radius of circle)
In right triangle CMO;
${{\left( CM \right)}^{2}}+{{\left( OM \right)}^{2}}={{\left( OC \right)}^{2}}$
${{\left( \dfrac{CD}{2} \right)}^{2}}+{{\left( {{r}_{2}} \right)}^{2}}={{r}^{2}}.........\left( 2 \right)$ (OC = r = radius of circle)
From equation (1) and (2);
${{\left( \dfrac{AB}{2} \right)}^{2}}+{{\left( {{r}_{1}} \right)}^{2}}={{\left( \dfrac{CD}{2} \right)}^{2}}+{{\left( {{r}_{2}} \right)}^{2}}$
We know that ${{r}_{1}}<{{r}_{2}}$, so for the LHS to be equal to RHS;
${{\left( \dfrac{AB}{2} \right)}^{2}}>{{\left( \dfrac{CD}{2} \right)}^{2}}$
Taking the square root of both side of equation, we will get;
$\Rightarrow \dfrac{AB}{2}>\dfrac{CD}{2}$
Multiplying both sides by ‘2’, we will get;
$\Rightarrow AB> CD$ Proved.