Question

Which is the item having maximum expenditure?

A. Bricks
B. Labour
C. Cement
D. Steel

Answer 1

Hint:
First, we will observe all the angles associated with the respective fields, then we will find the percentage of the total expenditure from the given pie chart. After that, the one with the maximum percentage would have the maximum expenditure. Hence, that would be our answer.

Complete step by step solution:
In a pie chart, the percentage of a particular field with respect to the total fields is given by:
If the field has an angle $\theta $ associated with it in a pie chart, then the percentage of that field is given by,
 ${\% _{field}} = \dfrac{\theta }{{360}} \times 100$ … (1)

Hence, now we will use this formula in our given pie chart.

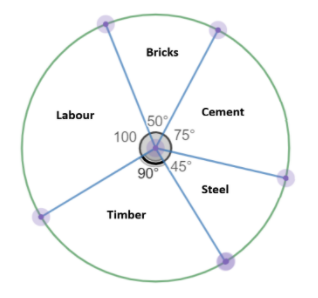
For Bricks the angle intercepted is $50^\circ $ ,
Hence, for bricks, put $\theta = 50^\circ $ in (1), we get

 $ \Rightarrow {\% _{Bricks}} = \dfrac{{50}}{{360}} \times 100$
On simplification we get,
 $ \Rightarrow {\% _{Bricks}} = \dfrac{{5000}}{{360}}$
Hence, we have,
 $ \Rightarrow {\% _{Bricks}} = 13.88$ …(2)

For Labour the angle intercepted is $100^\circ $ ,
Hence, for labour, put $\theta = 100^\circ $ in (1), we get

 $ \Rightarrow {\% _{Labour}} = \dfrac{{100}}{{360}} \times 100$
On simplification we get,
 $ \Rightarrow {\% _{Labour}} = \dfrac{{10000}}{{360}}$
Hence,
 $ \Rightarrow {\% _{Labour}} = 27.78$ …(3)

For Cement the angle intercepted is $75^\circ $ ,
Hence, for cement, put $\theta = 75^\circ $ in (1), we get

 $ \Rightarrow {\% _{Cement}} = \dfrac{{75}}{{360}} \times 100$
On simplification we get,
 $ \Rightarrow {\% _{Cement}} = \dfrac{{7500}}{{360}}$
Hence,
 $ \Rightarrow {\% _{Cement}} = 20.83$ …(4)
For Steel the angle intercepted is $45^\circ $,
Hence, for labour, put $\theta = 45^\circ $ in (1), we get

 $ \Rightarrow {\% _{Steel}} = \dfrac{{45}}{{360}} \times 100$
On simplification we get,
 $ \Rightarrow {\% _{Steel}} = \dfrac{{4500}}{{360}}$
Hence,
 $ \Rightarrow {\% _{Steel}} = 12.5$ …(5)

From (2),(3),(4) and (5) we observe that
 ${\% _{Labour}} > {\% _{Cement}} > {\% _{Bricks}} > {\% _{Steel}}$
So Labour is the item having maximum expenditure.

Hence, B is the correct answer.

Note:
In these types of questions, where the maximum field is asked by giving a pie chart, we observe that the angle intercepted by the field is directly proportional to the value field. Hence, in the above question we could have directly said that since Labour has the maximum angle intercepted in the given pie chart, Labour would be our final answer.