Question

Which figure is an example of a chord?
Figure 1:

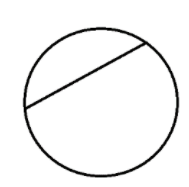
Figure 2:

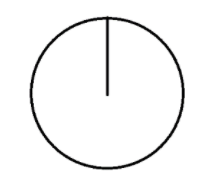
Figure 3:

Figure 4:

A. figure 4
B. figure 1
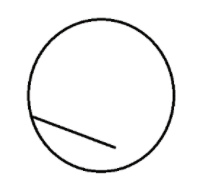
C. figure 3
D. figure 2

Answer 1

Hint:A circle has many parts. For example-radius, diameter, secant, segment, chord, tangent etc. To answer this question, we need to know definitions of all these parts.
Radius: A radius is a line drawn from the center of the circle to the boundary. A radius is a parameter which defines a circle.
Diameter: A line segment that joins any two points on the circle and also passes through the center is called a diameter.
Chord: A chord is a line segment that joins any two points on the circle.
There are other parts like segment, sector etc.

Complete step by step answer:
Let’s first know the definition of a chord.
CHORD: The line segment joining two points on a curve (in this case, circle) is called a chord. We can also say that a chord is a line segment whose endpoints lie on the curve.
Here’s a figure that shows all the different parts of a circle.

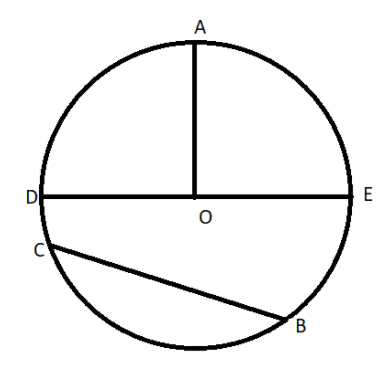
$OA$ = radius
$DE$ = diameter….(which is basically a chord passing through the center of the circle)
$BC$ = chord
Every diameter is a chord but every chord is not a diameter.A diameter is the longest chord in a circle.The figure that perfectly depicts a chord is Figure (1).
Figure 2 depicts a radius.
Figure 3 depicts a tangent.
Figure 4 is just a line segment drawn from point in the interior of the circle to a point on the boundary.

Hence, the right answer is option B.

Note:Students should be careful while selecting the option because the options are misleading.Knowing the definitions of the parts of a circle will be very beneficial for solving such questions. Every part of a circle has a significance. For example, a radius or a diameter can be used to find both the circumference and area of a circle. The formula of area is $\pi {r^2} = \pi \left( {\dfrac{{{d^2}}}{4}} \right)$. A tangent is always perpendicular to a line drawn from the center of the circle. Diameter always suspends an angle of 90° in the semi-circle and so on. Remembering the basic concepts will help us understand concepts like cyclic quadrilateral etc.