Question

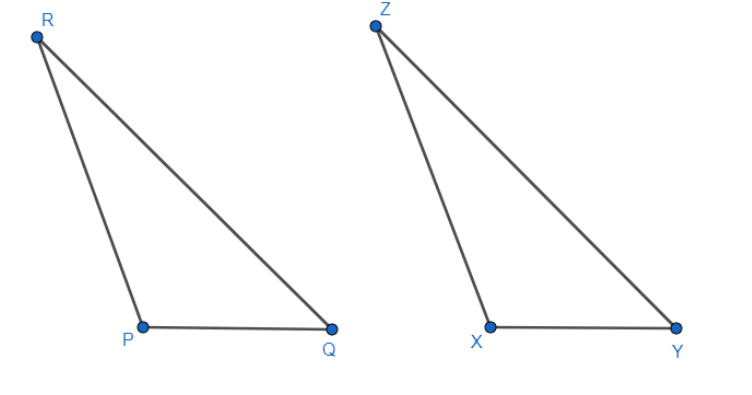
Which congruence criterion can be used for the following?
Given: $ RP=ZX,RQ=ZY,\angle PRQ=\angle XZY $ . So, $ \Delta PQR=\Delta XYZ $ .

Answer 1

Hint: We first explain the possible congruence criterion. We use SAS and show the conditions for the given information. We place the values of sides and in between angles to find the congruence.

Complete step-by-step answer:
In the given equality forms we have two equal sides of $ RP=ZX,RQ=ZY $ and one equal angle in between those equal sides
$ \angle PRQ=\angle XZY $ for $ \Delta PQR,\Delta XYZ $ respectively.
There are four types of congruence criterion and they are SSS, SAS, AAS, RHS.
For the above information we use SAS. The main condition for this congruence criterion is that the angle definitely has to be in between those two sides.
$ RP=ZX,RQ=ZY,\angle PRQ=\angle XZY $ for $ \Delta PQR,\Delta XYZ $ satisfies the conditions.
Two equal sides for $ \Delta PQR,\Delta XYZ $ are $ RP=ZX,RQ=ZY $ respectively. The angle $ \angle PRQ=\angle XZY $ in between those equal sides is also satisfies the condition.
Therefore. We got $ \Delta PQR=\Delta XYZ $ using the congruence criterion SAS.
So, the correct answer is “SAS”.

Note: Side Angle Side (SAS) is a rule used to prove whether a given set of triangles are congruent. In this case, two triangles are congruent if two sides and one included angle in a given triangle are equal to the corresponding two sides and one included angle in another triangle.