Question

When $\tan x=1$, what does $x$ equal?

Answer 1

Hint: We first find the principal value of x for which $\tan x=1$. In that domain, equal value of the same ratio gives equal angles. We find the angle value for x. At the end we also find the general solution for the equation $\tan x=1$.

Complete step-by-step answer:
It’s given that $\tan x=1$. We need to find x for which $\tan x=1$.
We know that in the principal domain or the periodic value of $-\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2}$ for $\tan x$, if we get $\tan a=\tan b$ where $-\dfrac{\pi }{2}\le a,b\le \dfrac{\pi }{2}$ then $a=b$.
We have the value of $\tan \left( \dfrac{\pi }{4} \right)$ as 1. $-\dfrac{\pi }{2}<\dfrac{\pi }{4}<\dfrac{\pi }{2}$.
Therefore, $\tan x=1=\tan \left( \dfrac{\pi }{4} \right)$ which gives $x=\dfrac{\pi }{4}$.
We also can show the solutions (primary and general) of the equation $\tan x=1$ through a graph. We take $y=\tan x=1$. We got two equations: $y=\tan \left( x \right)$ and $y=1$. We place them on the graph and find the solutions as their intersecting points.

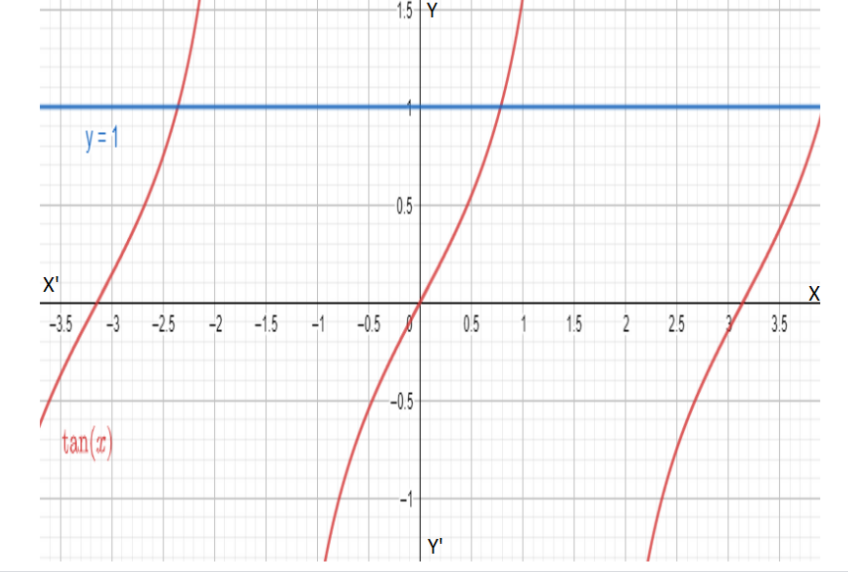
We can see the primary solution in the interval $-\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2}$ is the point A as $x=\dfrac{\pi }{4}$.
All the other intersecting points of the curve and the line are general solutions.
So, the correct answer is “ $x=\dfrac{\pi }{4}$”.

Note: Although for elementary knowledge the principal domain is enough to solve the problem. But if mentioned to find the general solution then the domain changes to $-\infty \le x\le \infty $. In that case we have to use the formula $x=n\pi +a$ for $\tan \left( x \right)=\tan a$ where $-\dfrac{\pi }{2}\le a\le \dfrac{\pi }{2}$. For our given problem $\tan x=1$, the general solution will be $x=n\pi +\dfrac{\pi }{4}$. Here $n\in \mathbb{Z}$.