Question

What is the vertex of $y={{x}^{2}}+6x+5$ ?

Answer 1

Hint: From the equation we can see that after plotting the given quadratic equation we will get some kind of parabola. We also know that the vertex of that parabola would be the minimum value of that parabola.

Complete step-by-step solution:
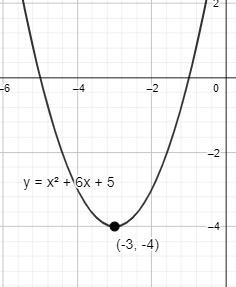
Now we can see that from the given equation we will get a parabola opening up and its vertex will be the minimum value of this parabola. Axis of symmetry for the same is the vertical line along the vertex.
In order to find the minimum value we will find the derivative of the given function as $f'(x)=2x+6$ now keeping it equal to zero will give us the value of x at which the derivative is zero therefore, x=-3 and since minimum value is one of the extrema value so it will be at critical points since we know that polynomials are infinitely differentiable so the only critical that will occur will be at the point where the derivative is zero which is -3.
Also, we can see that the factors of the quadratic equations are $y=(x+1)(x+5)$ so the x-intercepts are at -1 and -5 and similarly the y-intercept is at 0.
Thus the required vertex is at $\left(-3,f\left(-3\right) \right)$.
Now $f(-3)={{(-3)}^{2}}+6(-3)+5$
Which is equal to -4.
Therefore the coordinates of the vertex are $(-3,-4).$
The axis of symmetry is $x=-3.$

Note: Remember formula of conic section and just simply apply them. It is a direct question. Using the proper form of equation and comparing it with the general form of equation of the curve is necessary to avoid errors.