Question

What is the vertex of $y=2{{x}^{2}}+8x-3$?

Answer 1

Hint: Compare the given equation with the general form of a parabola as: - \[y=a{{x}^{2}}+bx+c\]. Find the respective values of a, b and c. Now, find the discriminant of the given quadratic equation by using the formula: - \[D={{b}^{2}}-4ac\], where D = discriminant. Write the expression as: -\[y=a\left[ {{\left( x+\dfrac{b}{2a} \right)}^{2}}-\dfrac{D}{4{{a}^{2}}} \right]\] and convert it into the form \[\left( y+\dfrac{D}{4a} \right)=a\left[ {{\left( x+\dfrac{b}{2a} \right)}^{2}} \right]\]. The vertex of the parabola will be given as \[\left( \dfrac{-b}{2a},\dfrac{-D}{4a} \right)\].

Complete step-by-step solution:
Here we have been provided with the quadratic equation: - $y=2{{x}^{2}}+8x-3$ and we are asked to find its vertex. First we need to write the vertex form of this quadratic equation using completing the square method.
Clearly the given equation is the general form of a parabola whose vertex we need to determine. The vertex of a parabola \[y=a{{x}^{2}}+bx+c\] is a point where its maxima or minima lie depending on the case that the parabola is opening upward or downward. Also, the vertex is the point through which the vertical line passing denotes the line of symmetry.
Any quadratic equation of the form \[y=a{{x}^{2}}+bx+c\] can be simplified as \[y=a\left[ {{\left( x+\dfrac{b}{2a} \right)}^{2}}-\dfrac{D}{4{{a}^{2}}} \right]\] using completing the square method and then it can be further written as \[\left( y+\dfrac{D}{4a} \right)=a\left[ {{\left( x+\dfrac{b}{2a} \right)}^{2}} \right]\]. Here, ‘D’ denotes the discriminant. The vertex is then given as \[\left( \dfrac{-b}{2a},\dfrac{-D}{4a} \right)\]. Now, on comparing $y=2{{x}^{2}}+8x-3$ with the general form we get,
\[\Rightarrow \] a = 2, b = 8, c = -3
Applying the formula for discriminant of a quadratic equation given as \[D={{b}^{2}}-4ac\] we get,
\[\begin{align}
  & \Rightarrow D={{\left( 8 \right)}^{2}}-4\left( 2 \right)\left( -3 \right) \\
 & \Rightarrow D=64+24 \\
 & \Rightarrow D=88 \\
\end{align}\]
So we can write the equation of the parabola as: -
\[\begin{align}
  & \Rightarrow y=2\left[ {{\left( x+\dfrac{8}{2\times 2} \right)}^{2}}-\dfrac{88}{4\times {{\left( 2 \right)}^{2}}} \right] \\
 & \Rightarrow y=2\left[ {{\left( x+2 \right)}^{2}}-11 \right] \\
 & \Rightarrow \left( y+22 \right)=2{{\left( x+2 \right)}^{2}} \\
\end{align}\]
Hence, the vertex of the parabola is $\left( -2,-22 \right)$.

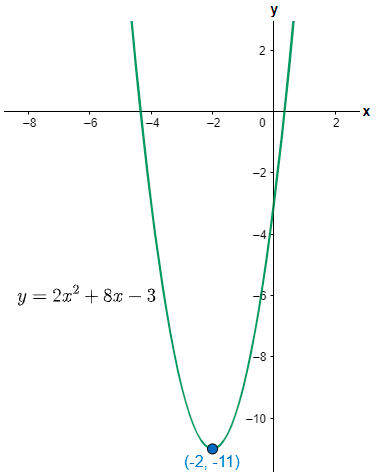
Note: Note that the equation \[\left( y+\dfrac{D}{4a} \right)=a\left[ {{\left( x+\dfrac{b}{2a} \right)}^{2}} \right]\] is known as the vertex form of the parabola. If we are asked to determine if the parabola is opening upward or downward then we can say that it is opening upward because the value of a is 2 which is positive. The point $\left( -2,-22 \right)$ denotes the minimum value of the parabola which is y = -22 and the point of minima is x = -2.