Question

What is the slope of \[x=-1\]?

Answer 1

Hint: Slope of a line is a number that describes the both the direction and steepness of the line. \[x=-1\] is a vertical line parallel to y axis and passes through \[\left( -1,0 \right)\]. Since \[x=-1\] is parallel to the y-axis, its slope is equal to the y-axis. We will use slope formula \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\] where \[m\]is the slope,\[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\]are two points on the line equation.

Complete step-by-step answer:
From the question we were given the equation of line \[x=-1\] and we were asked to find the slope of the line.
In mathematics, the slope of the line is a number that describes the both the direction and steepness of the line.
Slope is also called the gradient of the line.
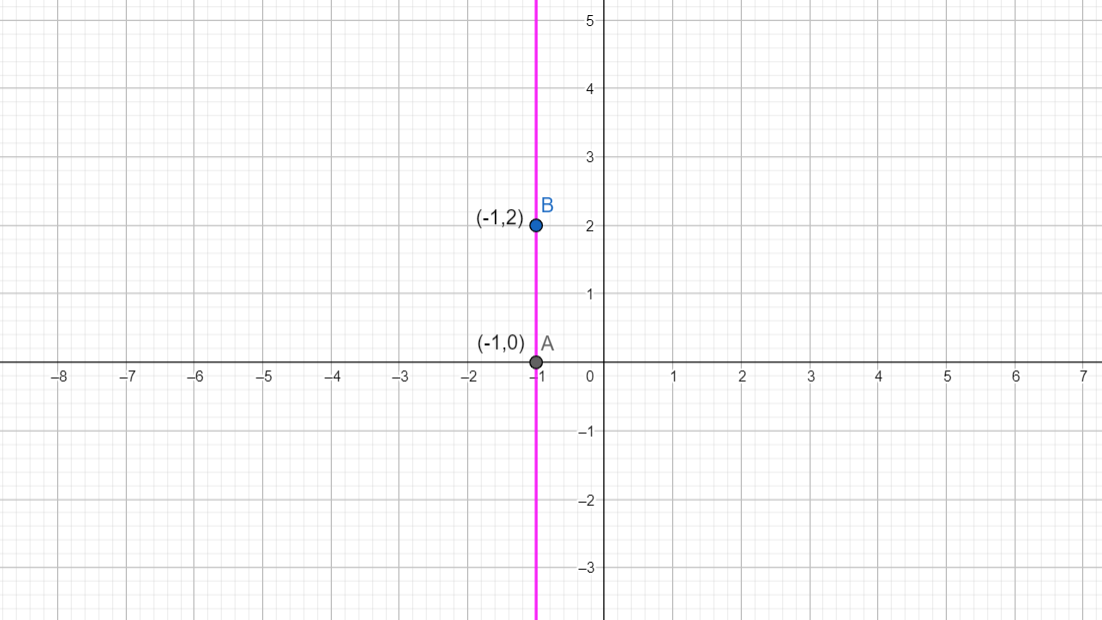
Let us try to solve the slope of the line \[x=-1\] by taking two points on the line.
\[A\left( -1,0 \right)\] is the point where the line intersects the x-axis.
\[B\left( -1,2 \right)\]is the point on the line.
\[A\left( -1,0 \right)\] and \[B\left( -1,2 \right)\] are known points on the line \[x=-1\].

\[\begin{align}
  & \Rightarrow \left( {{x}_{2}},{{y}_{2}} \right)=\left( -1,0 \right) \\
 & \Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( -1,2 \right) \\
\end{align}\]
So now We will use slope formula \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\] to find out the slope.
\[\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]…………….(1)
Now substitute the corresponding values in equation (1)
\[\Rightarrow m=\dfrac{0-2}{(-1)-(-1)}\]
If we subtract \[-1\]from \[-1\], the resultant will be zero
\[\Rightarrow m=\dfrac{-2}{0}\]
In fraction, denominator cannot be zero. If we ever have zero in the denominator, all we can say that the fraction is undefined.
In \[m=\dfrac{-2}{0}\], we have a denominator as zero. So here \[m\] is undefined.
So, the slope of line \[x=-1\] is undefined.

Note: Students may have the misconception that fraction having denominator zero is infinite but actually it is undefined. Students should be careful while doing calculations because small calculation errors can make getting the slope of line equation \[x=-1\] wrong.