Question

What is the slope of $ x = - 8 $ ?

Answer 1

Hint: The given equation is for a straight vertical line. Now, slope means the change in x over change in y, also represented by ratio of vertical rise and horizontal distance. In our question, the change in x over y is 0. So let us find out the slope of the given equation.

Complete step by step solution:
In this question, we have to find out the slope of equation $ x = - 8 $ .
First of all, let us understand what slope is.
If the inclination is $ \theta $ , then $ \tan \theta $ is known as the slope of a straight line. The slope is the ratio between the vertical rise and the horizontal distance.
Basically, slope is the change in y with change in x.

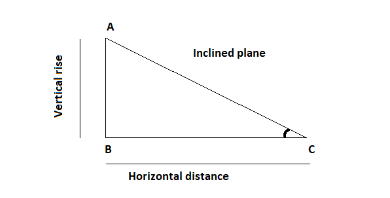
In the above figure, AB is the vertical rise, BC is the horizontal distance and AC is the inclined plane and $ \angle ACB = \theta $ .
So, we can find the slope by
slope $ = \dfrac{{vertical\;rise}}{{horizontal\;dis\tan ce}} = \dfrac{{AB}}{{BC}} = \tan \theta $
Now, to find the slope of $ x = - 8 $ , let us draw the graph firstly.

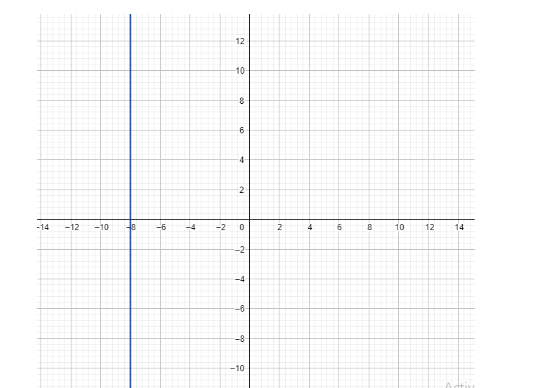
Here, observe that $ x = - 8 $ is the equation of a straight vertical line. The change in x over change in y Is 0 as the value of x is fixed at $ x = - 8 $ .
Hence, x is always going to be 0. So, the slope is going to be $ \dfrac{y}{0} $ and since y cannot be divided by 0, the slope of this line and every other vertical line will be undefined.

Note: The slope of a line will be positive if the line makes an acute angle in anti-clockwise direction with the x-axis.
2) The slope of a line will be negative if the line makes an obtuse angle in the anti-clockwise direction with x-axis or acute angle in clockwise direction with x-axis.