Question

What is the formula of Pythagoras?

Answer 1

Hint: Pythagoras or Pythagorean theorem is one of the most fundamental theorems in mathematics and it gives the relationship between the three sides of a right-angled triangle. For the formula of Pythagoras, we will take, hypotenuse, base and perpendicular of a right-angled triangle and therefore form a relation between them.

Complete step by step solution:
The Pythagoras theorem gives the relationship between the three sides of a right-angled triangle. Right-angled triangle is a type of triangle where one of its angles is a right angle, i.e., $90^\circ .$ In the right-angled triangle, Hypotenuse is the side, which is opposite to the angle $90^\circ .$ One side which is adjacent to right angle is perpendicular, another side which is adjacent to the right angle is called base, these both sides are together called legs of the triangle.
Let us construct a figure of a right-angled triangle to understand better.

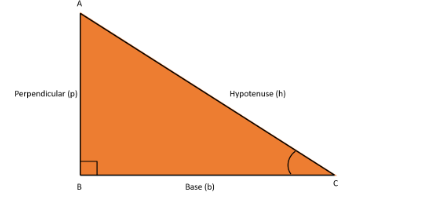
From the figure we can see that, AC, the longest side is Hypotenuse, AB is perpendicular, while BC is base.
The Pythagoras theorem states that the square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle, i.e.,
 \[{\left( {Hypotenuse} \right)^2} = {\text{ }}{\left( {Perpendicular} \right)^2}{\text{ }} + {\text{ }}{\left( {Base} \right)^2}\]
Or from the figure here, \[A{C^2}{\text{ }} = {\text{ }}A{B^2}{\text{ }} + {\text{ }}A{C^2}\]
Thus, the formula of Pythagoras is, \[{\left( {Hypotenuse} \right)^2} = {\text{ }}{\left( {Perpendicular} \right)^2}{\text{ }} + {\text{ }}{\left( {Base} \right)^2}\] .
So, the correct answer is “ \[{\left( {Hypotenuse} \right)^2} = {\text{ }}{\left( {Perpendicular} \right)^2}{\text{ }} + {\text{ }}{\left( {Base} \right)^2}\] .”.

Note: The statement of Pythagoras theorem can also be stated as, the sum of the squares of the two legs of a right-angled triangle is equal to the square of its hypotenuse.
And also, students should note that Pythagoras theorem is only applicable in right-angled triangles.