Question

What is the exact value of \[\sec {45^{}}\]?

Answer 1

Hint: Here we are asked to find the value of the secant of angle $45^\circ $ . In a right-angled triangle, the secant of an attitude is the ratio of duration of the hypotenuse to the period of the adjacent side. Trigonometry values of various ratios, which include sine, cosine, tangent, secant, cotangent and cosecant are used in the hassle.

Complete answer:
We aim to find the value of \[\sec {45^{}}\] from the trigonometric identities we know that $\cos = \dfrac{{\text{Adjacent side}}}{{\text{Hypotenuse}}}$ and secant can be written as $\sec = \dfrac{1}{{\cos }} = \dfrac{{hypotenuse}}{{adjacent}}$ . Let us draw a right-angle triangle for better explanation with an angle $45^\circ $.

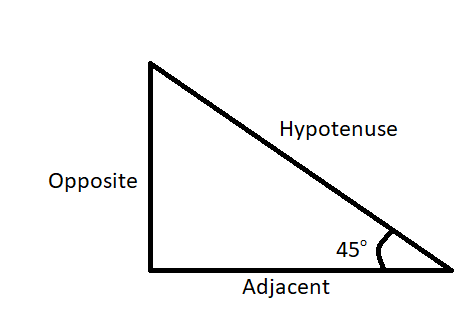
First of all, we have to look at the values of \[\cos \] in different angles.
\[\cos {0^ \circ } = 1 \]
\[\cos {30^ \circ }\dfrac{{\sqrt 3 }}{2} \]
\[\cos {45^ \circ } = \dfrac{1}{{\sqrt 2 }} \]
\[\cos {60^ \circ } = \dfrac{1}{2} \]
\[\cos {90^ \circ } = 0\]
From our trigonometric knowledge, we know that the secant function is also the reciprocal of the cosine function.
Hence, we can write $sec x$ as \[\dfrac{1}{{\cos x}}\]
Here we are given \[x = 45\]
To find the value of \[sec{\text{ }}45^\circ \] we can replace with \[x\] with \[{45^ \circ }\]
Therefore, we get,
\[sec{\text{ }}45^\circ {\text{ }} = {\text{ }}\dfrac{1}{{\cos {{45}^ \circ }}}\]
We know that \[\cos {45^ \circ } = \dfrac{1}{{\sqrt 2 }}\]
Hence substituting the value:
\[\sec {45^ \circ } = \dfrac{1}{{\dfrac{1}{{\sqrt 2 }}}}\]
\[\sec {45^ \circ } = \sqrt 2 \]

Therefore the exact value of \[\sec {45^{}}\] is \[\sqrt 2 \].

Additional Information:
Trigonometry values of different ratios, which include, sine, cosine, tangent, secant, cotangent and cosecant deal with the measurement of lengths and angles of the right-attitude triangle. The values of trigonometric functions are commonly used to solve trigonometry troubles. Trigonometry deals with the measurement of angles and troubles related to angles. The time period trigonometry is derived from a Latin word. Trigonometric formulation, symptoms are widely used within the area of mathematics.

Note:
Trigonometry values are all approximately the observations of well-known angles for a given triangle with respect to trigonometric ratios. The word ‘trigon’ means triangle and ‘matron’ means ‘size’. It’s one of the primary concepts and part of geometry, in which the relationship between angles and aspects of a triangle is defined. Trigonometry is an essential part of arithmetic and is widely utilized in fixing hassle. A thorough understanding of trigonometric formulas is a vital part of fixing such troubles.