Question

What is \[\text{sin x}\]equals to?

Answer 1

Hint:Before starting this problem, we need to know about the concept of trigonometry and its trigonometric ratios with their definitions. And define the \[\text{sin x}\]and its formula with their importance.

Complete step-by-step solution:
Trigonometry is the branch of mathematics which is basically concerned with specific function of angles, their applications and their calculations.
There are six basic trigonometric ratios for the right-angled triangle. They are sin, cos, tan, cosec, sec, cot which stands for Sine, Cosine, Cosecant, Tangent, Secant respectively. Sine and Cosine are basic trigonometric ratios which tells about the shape of the right triangle.

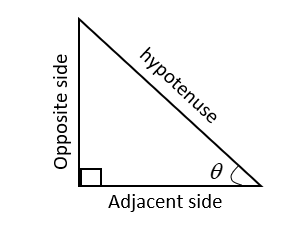
If we consider the above right-angled triangle, a right-angled triangle containing one of its angles is \[{{90}^{\circ }}\],hypotenuse is the longest side, which is one opposite to the right angle. The adjacent side is the side which is between the angle to be determined and the right angle. From the figure,
\[\text{sin}\theta \text{=}\frac{\text{opposite side}}{\text{hypotenuse}}\]
We can also write
\[\tan \theta =\dfrac{\sin \theta }{\cos \theta }\]
Then \[\sin \theta \] is equals to
\[\sin \theta =\tan \theta \cdot \cos \theta \]
The sine is defined as it is the trigonometric function which is equal to the ratio of length of opposite side to the length of the hypotenuse.
Some basic relations of sine are
In terms of ‘tan’,
\[\sin \theta =\dfrac{2\tan \dfrac{\theta }{2}}{1+{{\tan }^{2}}\dfrac{\theta }{2}}\]
In terms of ‘cos’
\[\text{sin }\theta \text{=cos}\left( 90-\theta \right)\]

Note: Students making mistakes due to quickly relating something in place of another. Students do not understand how to approach a given trigonometrical problem from the concept. Students make errors in applying identities and also do errors in calculations. Understanding the trigonometric based question is also a time taking process.