Question

What is 4pi in degrees?

Answer 1

Hint: For solving this type of question you should know about the converting radians to degrees, and it is done by multiplying the radian value by \[\dfrac{180}{\pi }\]. Pi radians are equal to 180 degrees. And one radian is equal to 57.295779513 degrees. Since we know that a circle contains \[{{360}^{\circ }}\] and a pi is equal to \[{{180}^{\circ }}\]. So, a circle is of \[2\pi \] radian value.
According to the question we have to calculate the value of \[4\pi \] in degrees.

Complete step by step answer:
Here, if we see then one radian contains \[{{180}^{\circ }}\] and that is equal to half circle’s angle.
So, for making a complete circle it is necessary to be \[2\pi \] radians.
Generally, one radian is the angle which is made at the centre of the circle by an arc whose length is always equal to the radius of the circle.

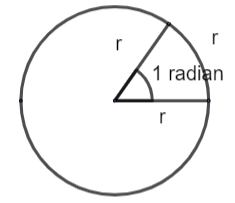
It is shown in the figure that one radian has all the same measurements as radius and arc. The radian is a unit for measuring of the angles which is used mainly in trigonometry. If we take any full circle then it contains more than 6 radians.
For calculating this:
as we know that \[1{{\pi }^{C}}={{180}^{\circ }}\]
To convert radian into degrees, we will multiply by \[\dfrac{180}{\pi }\].
So, \[4{{\pi }^{C}}={{\left( 4\pi \times \dfrac{180}{\pi } \right)}^{\circ }}\]
       \[\begin{align}
  & 4{{\pi }^{C}}={{\left( 4\times 180 \right)}^{\circ }} \\
 & 4{{\pi }^{C}}={{720}^{\circ }} \\
\end{align}\]
So, the degree value of \[4\pi \] radian is 720.

Note: As seen in the figure above a radian is defined by an arc of a circle. And the length of the arc is always equal to the radius of the circle. Because there is a fixed size of radius for every circle so the radian also has a fixed value. Thus, you can convert the radian into degrees and also you can calculate degrees into radian.