Question

What is \[|| < 4,9, - 8 > ||\] ?

Answer 1

Hint: In order to solve this question, first we will understand the concept of vector and the magnitude of a vector. Then we will understand the meaning of the double vertical lines on both sides and finally we will be able to find the answer.

Complete step by step answer:
A vector quantity is a quantity which has both magnitude and direction. The length of the vector represents the magnitude and the arrowhead points in the direction. We are well aware of the fact that a vector is an object which has magnitudes as well as it has a direction. So, if we have to find the magnitude of a vector then we have to calculate the length of any given vector. The various quantities such as velocity, displacement and force are examples of vector quantities.

The vector given in this question can be represented as,

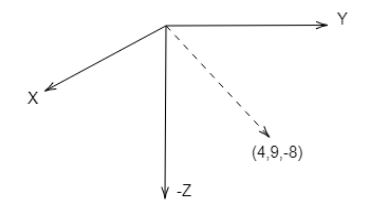
In this particular question, the double vertical lines represent that in this question, we have to find the magnitude of this vector. We know that the magnitude of a vector is the square root of the sum of the squares of all the three components of a vector. So, the magnitude of this vector is,
$l = \sqrt {{{(4)}^2} + {{(9)}^2} + {{( - 8)}^2}} $
$\Rightarrow l = \sqrt {16 + 81 + 64} $
On further solving this, we get,
$l = \sqrt {161} $
On finding the approximate value of the above root, we get,
$\therefore l = 12.7\,units$

Therefore, the magnitude or the length of this vector is $l = 12.7\,units$.

Note: It is important to note that in this question, although the vector is present in three dimensions, we have taken the square root, and not the cube root. When the vector is in two dimensions then also we take the square root. So, it does not matter whether the vector is in two dimensions or in three dimensions, we always take square roots.