Question

What is $20\text{ minutes}$ before $12\text{ pm}$ .

Answer 1

Hint: We need to find the time $20\text{ minutes}$ before $12\text{ pm}$ . For hour hand, the numbers will be read as such. But for the minute hand, from $12:00$, each line is numbered from one and completed one round and reaches $12:00$ in $60\text{ minutes}$ as there are $60$ such lines. After $60\text{ minutes}$, we say one hour is completed. From $12:00$ noon it is denoted as PM till the next $12:00$ night, which is denoted as AM. From $12:00$ night it is denoted as AM till the next $12:00$ noon, which is denoted as PM.

Complete step by step answer:
We need to find the time $20\text{ minutes}$ before $12\text{ pm}$ .
In a clock, there are twelve numbers starting from $1$.
Each number is separated by four lines each of one minute. Thus from one number to the adjacent number, for example, $12\text{ to 1}$ , the difference will be $5$ (four lines in between and the line that represents the adjacent number). Hence, each adjacent number differs by five minutes.
We know that for the hour hand, the numbers will be read as such. Also, we know that for the minute hand, from $12:00$, each line is numbered from one and completed one round and reaches $12:00$ in $60\text{ minutes}$ as there are $60$ such lines. After $60\text{ minutes}$, we say one hour is completed.
Now, for a 12-hour period system, we have AM = Ante meridiem is before noon and PM = Post meridiem is afternoon. From $12:00$ noon it is denoted as PM till the next $12:00$ night, which is denoted as AM. From $12:00$ night it is denoted as AM till the next $12:00$ noon, which is denoted as PM.

The figure shows $12:00\text{ pm}$ .

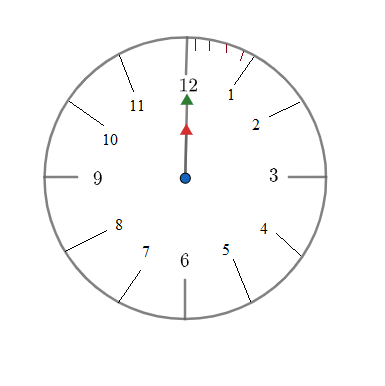
We need to find $20\text{ minutes}$ before $12\text{ pm}$ . Hence we will travel $20\text{ minutes}$ anti-clockwise.
Since, each number is of difference $5$ , moving $20\text{ minutes}$ backwards gives as follows:
$20\text{ minutes=}5+5+5+5$
Thus, we have
$5\text{ minutes backwards}=11:55$
Next $5\text{ minutes backwards}=11:50$
Next $5\text{ minutes backwards}=11:45$
Next $5\text{ minutes backwards}=11:40$

So time will be $11:40\text{ am}$ .
Hence, the answer is $11:40\text{ am}$
Note:
  Do not get confused with AM and PM. The timing system used here is 12-hours. For 24-Hour system, any hour time will be read from $13:00$ ($01:00\text{ pm}$ ) to $24:00$ ($12:00\text{ am}$ ).The answer to this question will be the same for a 24-hour time as the change happens before $01:00\text{ pm}$ and $12:00\text{ am}$.