Question

What does sinusoidal mean?

Answer 1

Hint: We use the concepts related to trigonometry and using those, we will solve this problem. Generally, trigonometry deals with angles and sides. We will define some functions like sine, and we will plot a graph of that function. And from this, we will find the meaning of sinusoidal.

Complete step by step answer:
In mathematics, trigonometry deals with ratios of sides in a right-angled triangle. In a right-angled triangle, the side opposite to the right-angle is called the hypotenuse. It is the side with the highest length in a right-angled triangle.

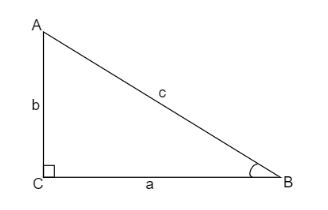
In this triangle, \[\vartriangle ABC\], the sine of angle ‘B’ is defined as the ratio of side opposite to it to hypotenuse.
\[ \Rightarrow \sin B = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} = \dfrac{b}{c}\]
The cosine of angle ‘B’ is defined as the ratio of side adjacent to it to hypotenuse.
\[ \Rightarrow \cos B = \dfrac{{{\text{Adjacent}}}}{{{\text{Hypotenuse}}}} = \dfrac{a}{c}\]
And tangent of angle ‘B’ is defined as the ratio of side opposite to it to side adjacent to it.
\[ \Rightarrow \tan B = \dfrac{{{\text{Opposite}}}}{{{\text{Adjacent}}}} = \dfrac{a}{c}\]

Now let us discuss in detail about sine function. Sine function range is from \[ - 1\] to \[1\] including both i.e., \[Range = \left[ { - 1,1} \right]\]. And it is a continuous function and differentiable at all points.This function is defined in the range \[\left( { - \infty ,\infty } \right)\], i.e., it is defined for all rational numbers.When we plot this function on a graph, we get the graph as follows.

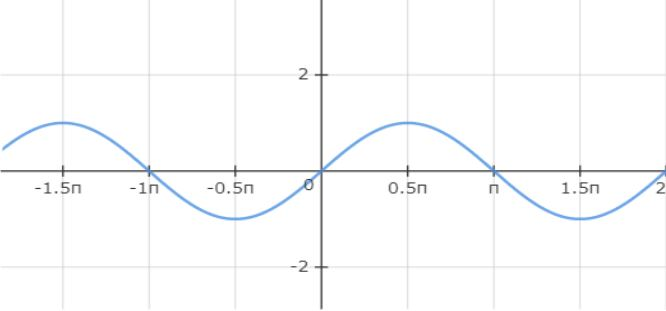
The curve that we got here is known as the ‘Sinusoidal Curve’. The distance from peak point (or) maximum point to the X-Axis is called the Amplitude. So, any wave or function containing this type of curve is said to be sinusoidal in nature. If we move this wave towards left or right by a phase of \[\dfrac{\pi }{2}\] or odd multiples of \[\dfrac{\pi }{2}\], we get another function which is a Cosine function.So, any function containing this cosine function wave is also said to be sinusoidal in nature.

Note: A sine function is an odd function i.e., if \[f(x) = \sin x\], then, \[f( - x) = - f(x)\].Though we change the amplitude or period of a sinusoidal wave, it will still be a sinusoidal wave. Sine function and the cosine function are just different by \[\dfrac{\pi }{2}\] radians. So, we can write that as \[\cos ({90^ \circ } - \theta ) = \sin \theta \].