Question

What does $\sec \pi/2$ equal?

Answer 1

Hint: To solve the question, the concept of trigonometric value should be known. The values of trigonometric values for certain numbers should be known. Details of the trigonometric function is required to solve the question.

Complete step by step answer:
To start with some details on the trigonometric function, $\sec $. We know that the trigonometric function $\sec x$ is the reciprocal of the other trigonometric function $\cos x$, this could be mathematically represented as
$\sec x=\dfrac{1}{\cos x}$…………………………………………………………. (i)
On applying the same formula to find value of the given question,
$\Rightarrow \sec \dfrac{\pi }{2}=\dfrac{1}{\cos \dfrac{\pi }{2}}$
With the help of the graph of $\cos x$ we know that
$\cos \dfrac{\pi }{2}=0$
On applying the fact in equation (i), we get
$\Rightarrow \sec \dfrac{\pi }{2}=\dfrac{1}{0}$
This is undefined,
$\therefore $ The value of $\sec \dfrac{\pi }{2}$is not defined.

Note: Calculation of the trigonometric function with a certain angle becomes much easier with the help of the graph. Minimum and maximum value of the function could easily be known to us with the help of graphs. This is the graph of $\sec $(angle). On seeing the above graph it can be inferred that at angle 0 the functions sec of zero is the minimum value, 1. It is clear from the graph that at angle $\dfrac{\pi }{2}$,which is the midpoint of the function $\sec $ is undefined.

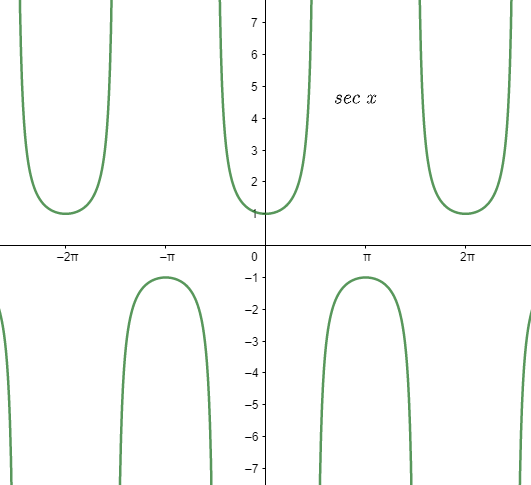
Now, let us see the graph of $\cos x$

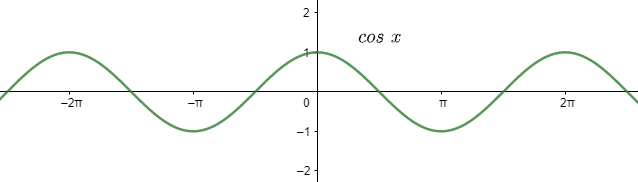
On differentiating both the graph we can at least infer that the trigonometric function $\sec $ for any angle is reciprocal of $\cos $ for the same angle, which means
$\sec x=\dfrac{1}{\cos x}$
In this question the angle is in radian but sometimes the angle given is in the form of degree too , so we should know to convert the angle in radian to degree. So we can convert the unit of the angle as
$\pi ={{180}^{\circ }}$ and then as per the question’s demand the further solving would take place.