Question

What are corresponding angles?

Answer 1

Hint: First, we will need to know the corresponding angles. Corresponding angles are formed when the given two lines are crossed by another line. The angles created in matching corners at each intersection are the corresponding angle. When the two lines interest, at the point of their intersection an angle is formed, they form the base of geometry.

Complete step-by-step solution:
Types of angles are Acute angle, Right angle, Obtuse angle, Straight angle, Reflex angle, Right angle, Supplementary angle, Complementary angle, Adjacent angle and vertical angle.
Acute angle:
An acute angle is measured less than ${90^0}$. The measure of this angle is only at between ${0^0}$ to ${90^0}$.
It can be represented as

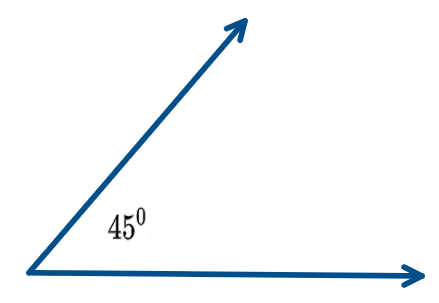
As we see using the diagram representation of the acute angle and it was not exceeding the angle of ninety degrees.
 Right angle:
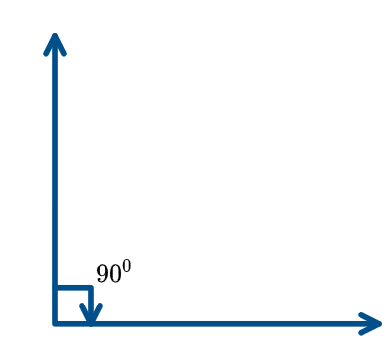
An angle that measures exactly ${90^0}$ is known as the right angle. When given two lines are perpendicular to each other.
The right angle can be represented as

Obtuse angle:
An angle that measures greater than ${90^0}$ is called the obtuse angle.
It will measure from the range of ${90^0}$ to ${180^0}$and obtuse angle can be also found out if we have the measure of acute angle
The obtuse angle can be represented as

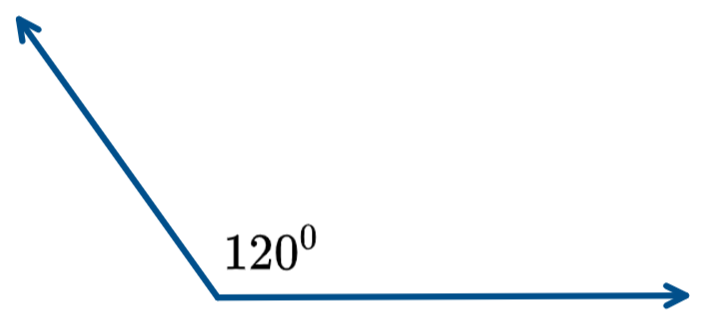
Obtuse angle measure = ${180^0}$- acute angle measures.
Hence the extended line will be given as \[{120^0} + {60^0} = {180^0}\]
Supplementary angle is the sum of the total of $2$angles is \[{180^0}\]
Complementary angles are the sum of the total of $2$angles that are \[{90^0}\]
Adjacent angles are the common arm and a common vertex.
Vertical angles are the two lines bisect, the angle that is created opposite to each other at the vertex.


Note: The straight angle measures exactly the \[{180^0}\]which is more like the straight line. Reflex angles are measured greater than \[{180^0}\] and less than \[{360^0}\].
It can be calculated by measuring the measure of acute angle from the given and it's complement of the acute angle on the other side. The total angle is \[{360^0}\]from the given circle. Hence there are $9$ corresponding angles.