Question

Weight of a body of mass m decreases by $1%$ when it is raised to height h above the earth’s surface. If the body is taken to a depth h in a mine, change in its weight is:
A. by $0.5%$ decrease
B. by $2%$ decrease
C. by $0.5%$ increase
D. by $1%$ increase

Answer 1

Hint: To find change in percentage of any quantity find its final value and its initial value. Take the difference of final and initial value and divide it with its initial value then multiply it by 100, to find change in percentage. The same approach we apply in our question.

Formula Used:
Acceleration due to gravity at height h above the earth’s surface is given by:
${{g}_{h}}=\dfrac{g}{{{\left( 1+\dfrac{h}{R} \right)}^{2}}}$
If $h$ $<<$ $R$
${{g}_{h}}=g\left( 1-\dfrac{2h}{R} \right)$
Acceleration due to gravity at depth d below the earth’s surface is given by:
${{g}_{d}}=g\left( 1-\dfrac{d}{R} \right)$
Where g is the acceleration due to gravity on earth’ and R is the radius of the earth.

Complete step by step answer:
Let the weight of the body on earth’s surface be $W$ and it is given by $W=mg$
Weight of the body at height h above the earth’s surface is ${{W}_{h}}$ , it is given by:
${{W}_{h}}=m{{g}_{h}}$
${{W}_{h}}=mg\left( 1-\dfrac{2h}{R} \right)$
Decrement in weight of the body is given by:
Percentage change $=\dfrac{{{W}_{h}}-W}{W}$
$\begin{align}
  & 1=\dfrac{{{W}_{h}}-W}{W} \\
 & 1=\dfrac{mg\left( 1-\dfrac{2h}{R} \right)-mg}{mg} \\
 & 1=\dfrac{-2h}{R} \\
 & \dfrac{-h}{R}=\dfrac{1}{2} \\
\end{align}$
Here the negative sign represents the decrement.
Now, the weight of the body at depth h below the earth's surface be ${{W}_{d}}$, and where ${{W}_{d}}=m{{g}_{d}}$
And the weight of the body on the earth’s surface is $W$i.e. $W=mg$
Percentage decrement $=\dfrac{{{W}_{d}}-W}{W}$
$\begin{align}
  & =\dfrac{mg\left( 1-\dfrac{d}{R} \right)-mg}{mg} \\
 & d=h \\
 & =\dfrac{-h}{R} \\
 & =\dfrac{1}{2}=0.5 \\
\end{align}$
Therefore percentage decrement below depth h is $0.5%$
Hence, option A. is the correct answer.
Note: The maximum value of acceleration due to gravity i.e. g is on the earth’s surface, below or above the earth’s surface the value of g decreases.

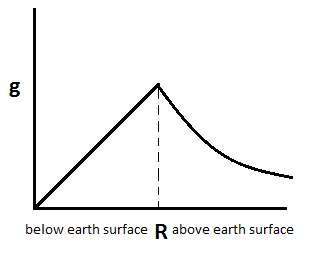
There is another case where value of g decreases is due to rotation of earth and is given by ${{g}_{r}}=g-{{\omega }^{2}}R{{\cos }^{2}}\lambda $
Where, $\omega $is angular velocity and $\lambda $is angle made by the equator and gravitational force due to gravity.
At equator $\lambda ={{0}^{0}}$ and at poles $\lambda ={{90}^{0}}$