Question

We have given \[sec\theta = 5\;\]and \[tan\theta = 2\sqrt 6 \], how do you find \[cot(90^ \circ - \theta )\] ?

Answer 1

Hint: We will try to find the relation of trigonometric ratios with the help of quadrants. We will assume that triangle ABC lies in the first quotient and find the value of \[cot(90^ \circ - \theta )\] with the help of basic identities of trigonometry and substitute the value from the given values of tan.

Complete step-by-step answer:
We will try to prove that $\cot \left( {{{90}^ \circ } - \theta } \right) = \tan \theta $
We will try to find the relation among all the trigonometric ratios of ${90^ \circ } - \theta $
We will use quadrants to calculate the value.
We know that all of the values in the first quadrant are positive. In the second quadrant only sin and cosec are positive. In the third quadrant we have tan and cot are positive while in the fourth quadrant cos and sec are positive.
We will assume that ${90^ \circ } - \theta $ lies in the first quadrant.
We know that in the first quadrant all are positive.
We will now find the value of \[cot(90^ \circ - \theta )\]

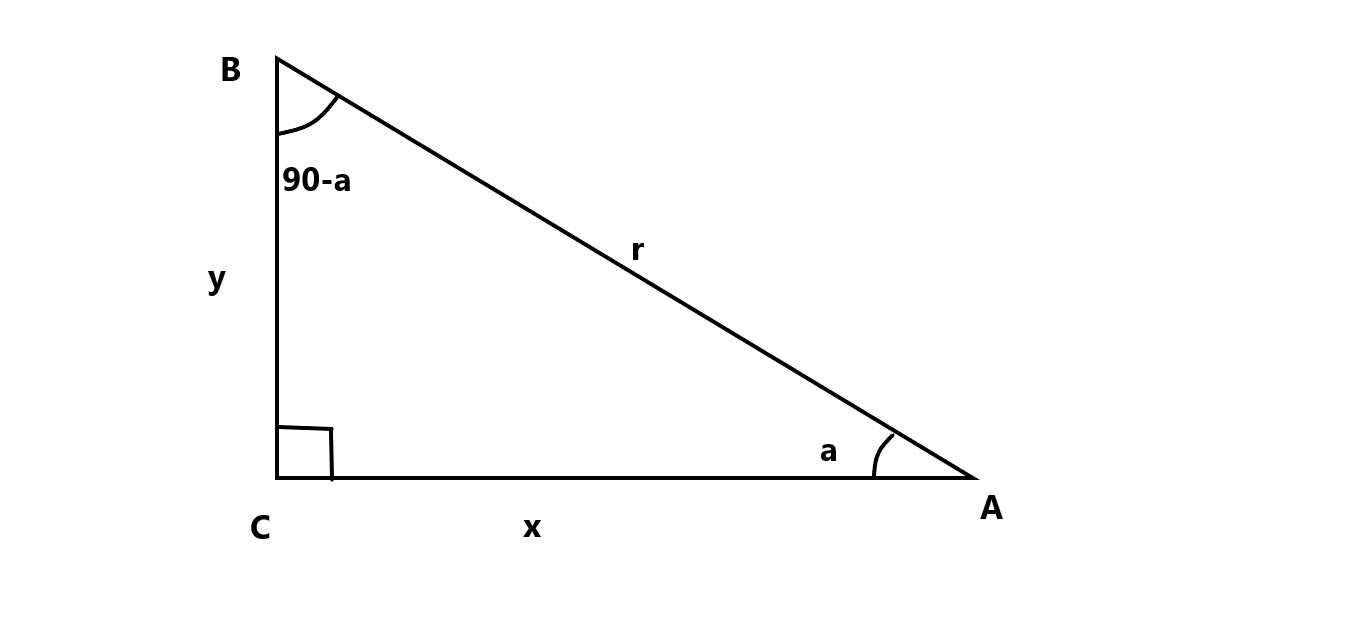
                                                                  Fig.1

In figure 1, we have left the value of sides.
We have assumed one angle as a, so the other angle will become 90-a.
We know that cot is the ratio of base and perpendicular while tan is ratio of perpendicular and base.
So, the value of $\tan a$ is
$ \Rightarrow \tan a = \dfrac{y}{x}$
Similarly, we will find the value of $\cot \left( {{{90}^ \circ } - a} \right)$
$ \Rightarrow \cot \left( {{{90}^ \circ } - a} \right) = \dfrac{y}{x}$
So, we have proved that $\cot \left( {{{90}^ \circ } - \theta } \right) = \tan \theta $
We have the value of \[tan\theta = 2\sqrt 6 \] .
 So, the value of $\cot \left( {{{90}^ \circ } - \theta } \right)$ is
$ \Rightarrow \cot \left( {{{90}^ \circ } - \theta } \right) = 2\sqrt 6 $
Hence, the value of $\cot \left( {{{90}^ \circ } - \theta } \right) = 2\sqrt 6 $ when we have given \[tan\theta = 2\sqrt 6 \] .

Note: We can also solve this question in one line if we are familiar with the property of trigonometry that $\cot \left( {{{90}^ \circ } - \theta } \right) = \tan \theta $ . we have to very careful while solving these types of question. These are trick questions as in the above question we didn’t use the value of sec for solution. These values are given to confuse us.