Question

We have $\Delta ABC$ and the point M such that $\overrightarrow {BM} = 2\overrightarrow {MC} $. How to determine x, y such that $\overrightarrow {AM} = x\overrightarrow {AB} + y\overrightarrow {AC} $?

Answer 1

Hint: Start the solution by first constructing a triangle according to the information given after this step apply triangle law to both of the sub triangles formed with the large triangle and then use the given information also. After a few calculations, compare it with the given equation and you get the values of x and y respectively.

Complete step by step solution:
We have been given the equation as $\overrightarrow {AM} = x\overrightarrow {AB} + y\overrightarrow {AC} $ where we have to determine the values of x and y respectively.
That is we have to find the scalar quantities of how many times $\overrightarrow {AB} $ and a scalar times $\overrightarrow {AC} $ will give us the value for $\overrightarrow {AM} $.

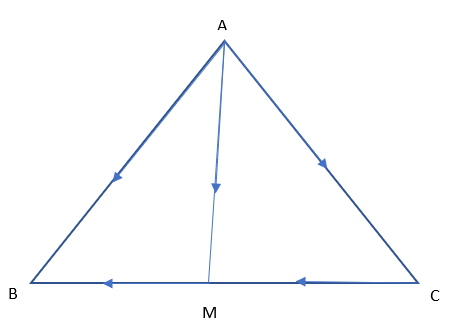
Let us first use the vector property to the $\Delta ABM$. Applying the vector property we get $\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} $
But we have been already given that $\overrightarrow {BM} = 2\overrightarrow {MC} $. So substituting this value in above equation we get $\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {MC} - - - (1)$
Now considering $\Delta AMC$ and applying triangle law we get
$\overrightarrow {AM} + \overrightarrow {MC} = \overrightarrow {AC} $
$ \Rightarrow \overrightarrow {MC} = \overrightarrow {AC} - \overrightarrow {AM} $
Substituting this value in equation (1) we get
\[\overrightarrow {AM} = \overrightarrow {AB} + 2\left( {\overrightarrow {AC} - \overrightarrow {AM} } \right)\] solving the above equation we get
\[
  \overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {AC} - 2\overrightarrow {AM} \\
   \Rightarrow \overrightarrow {AM} + 2\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {AC} \\
   \Rightarrow 3\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {AC} \\
 \]
Dividing both the sides of the equation by 3 we get
\[\overrightarrow {AM} = \dfrac{1}{3}\overrightarrow {AB} + \dfrac{2}{3}\overrightarrow {AC} \]
Hence comparing the above with the equation with $\overrightarrow {AM} = x\overrightarrow {AB} + y\overrightarrow {AC} $, we get
$x = \dfrac{1}{3}$ and $y = \dfrac{2}{3}$

Note: The use of vector property of additions is the most important part of the above sum without which you cannot proceed further. You just need to mention the triangle for which you are going to apply the vector law of addition. Also the signs of the vector changes if it’s direction is changed.