Question

Water is flowing through a cylindrical pipe, of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m/s. Determine the rise in the level of water in the tank in half hours.

Answer 1

HINT- Proceed the solution of this question, using the concept that the Volume of water filled in a cylindrical tank for a particular duration is equal to the volume of water flowed out in that duration from the pipe.
Complete Step-by-Step solution:

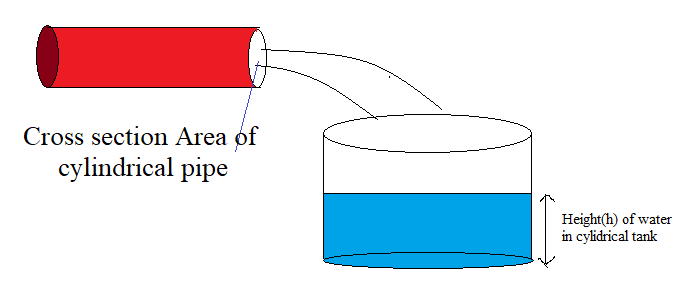
Diameter of cylindrical pipe having circular end = 2 cm
We know that, Diameter =$\dfrac{{{\text{Radius}}}}{2}\text{ }\& {\text{ 1 cm = 0}}{\text{.01 m}}$
 $\therefore $Radius ( ${{\text{r}}_1}$) of circular end of pipe = $\dfrac{2}{2} = 1{\text{ cm = }}{\text{.01 m}}{\text{.}}$
Area of cross-section = $\pi {{\text{r}}_1}^2 = \pi {(0.01)^2} = 0.0001\pi {\text{ }}{{\text{m}}^2}$
Speed of water = 0.4 m/s = 0.4 60 = 24 metre/min (using 1 second = $\frac{1}{{60}}$minute)
Volume of water that flows in 1 minute from pipe will be equal to Area of cross-section of cylindrical pipe multiplied by speed of flow of water through it.
So, Volume of water that flows in 1 minute from pipe$ = 24(\text{m}/\text{minute}) \times 0.0001\pi {\text{ }}{{\text{m}}^2} = 0.0024\pi {\text{ }}{{\text{m}}^3}$
So using unitary method,
Volume of water that flows in 30 minutes from pipe = $ = 30 \times 0.0024\pi {\text{ }}{{\text{m}}^3} = 0.072\pi {\text{ }}{{\text{m}}^3}$
Radius (r2) of base of cylindrical tank = 40 cm = 0.4 m $\left( {{\text{using }}1{\text{ cm = }}{\text{.01 m}}{\text{.}}} \right)$
Let the cylindrical tank be filled up to h m in 30 minutes.
We know that,
Volume of water filled in a cylindrical tank in 30 minutes is equal to the volume of water flowing out in 30 minutes from the pipe.
$\therefore {\text{ }}\pi {{\text{r}}_2}^2 \times {\text{h = 0}}{\text{.072}}\pi $
On putting Radius (r2) =0.4 m.
$ \Rightarrow \pi {(0.4)^2} \times {\text{h = 0}}{\text{.072}}\pi $
$ \Rightarrow \pi 0.16 \times {\text{h = 0}}{\text{.072}}\pi $
\[ \Rightarrow {\text{h = }}\dfrac{{{\text{0}}{\text{.072}}}}{{0.16}}\]
\[ \Rightarrow {\text{h = 0}}{\text{.45m or 45cm}}\]

Therefore, the rise in level of water in the tank in half an hour (or in 30 minutes) is 45 cm.

Note-
In this particular question, the main thing that we have kept in our mind is that the volume of water is going to remain the same, so we have to equalise the volume in two cases. But here we should also focus on units, like units of rate of flow of water whether it is m/sec or m/minute, unit of radius and heights whether those are in meter or centimetre. So keeping the same unit throughout the solution, we can avoid these silly calculation mistakes.