Question

Water is flowing at the rate 5Km/hr. through a pipe of diameter 14cm into a rectangular tank which is 50m long and 44m wide. Determine the time in which the level of the water in the tank will rise by 7cm.

Answer 1

Hint: In this particular question first draw the pictorial representation the above problem it will give us a clear picture of what we have to find out, then use the formula of the volume of cuboid is LBH, where symbols have their usual meaning, and the volume of the cylinder is $\pi {r^2}h$, where r is the radius and h is the height or length of the cylinder respectively, so use these concepts to reach the solution of the question.

Complete step-by-step answer:

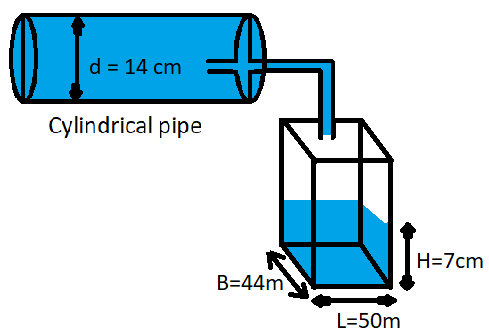
Given data:
Water is flowing at the rate 5Km/hr. through a pipe of diameter 14cm.
So the length of the cylindrical pipe is, h = 5Km = 5000m, [as, 1km = 1000m]
And we all know that radius is half of the diameter, so $r = \dfrac{d}{2} = \dfrac{{14}}{2} = 7cm$ = 0.07m, [as, 1m = 100cm]
Now as we know that the volume of the cylinder is $\pi {r^2}h$ cubic units where symbols have the usual meaning.
So the volume (${V_1}$) of the cylindrical pipe = $\pi {r^2}h$ = $\dfrac{{22}}{7}{\left( {0.07} \right)^2}\left( {5000} \right) = 77{\text{ }}{{\text{m}}^3}$
So the amount of water that will be flowed from the cylindrical pipe in one hour = 77 cubic meter/hour.
Now that water will flow into the rectangular tank.
So the amount of water that will be flowed from the cylindrical pipe in one hour into the rectangular tank should be equal.
Let the time it will take in which the level of the water in the tank will rise by 7cm be, t hours.
So, t multiplied by the volume of the cylinder = volume of the rectangular tank i.e. cuboid.
$ \Rightarrow t \times {V_1} = {V_2}$............ (1)
Now as we know that the volume of cuboid is LBH, where symbols have their usual meaning.
Now it is given that the rectangular tank is 50m long and 44m wide.
So L = 50m, and B = 44m.
Now the water in the tank will rise by 7cm = 0.07m.
So, H = 0.07m.
So the volume (${V_2}$) of the rectangular tank = $50\left( {44} \right)\left( {0.07} \right) = 154{\text{ }}{{\text{m}}^3}$
Now from equation (1) we have,
$ \Rightarrow t \times \left( {77} \right) = 154$
$ \Rightarrow t = \dfrac{{154}}{{77}} = 2$ Hours.
So it will take 2 hours.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall the formula of the volume of the cuboid as well as cylinder which are all stated above, o first find out the volume of the cylinder as above, then find out the volume of the rectangular tank as above, then the time take to fill the rectangular tank up to 7 cm height is time in hours multiplied by the volume of the cylindrical pipe and equal to the volume of rectangular tank so substitute the values as above, and simplify we will get the required answer, do not forget to change the units of the parameters into same units, otherwise we will get wrong answer.