Question

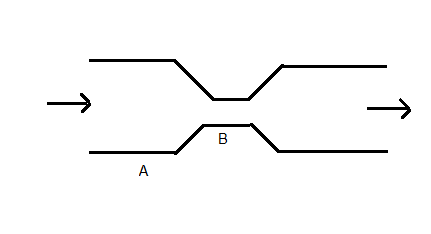
Water flows through a horizontal tube as shown in the figure. If the difference of heights of water column in the vertical tubes is h=0.02m, and the areas of cross section at A and B are \[4\times {{10}^{-4}}{{m}^{2}}\]
and \[2\times {{10}^{-4}}{{m}^{2}}\], respectively, then the rate of flow of water across any section is?
A- \[130\times {{10}^{-6}}{{m}^{3}}/s\]
B- \[146\times {{10}^{-6}}{{m}^{3}}/s\]
C- \[160\times {{10}^{-6}}{{m}^{3}}/s\]
D- \[170\times {{10}^{-6}}{{m}^{3}}/s\]

Answer 1

Hint: Generally the flow of water through a pipe is governed by many important theorems such as the equation of continuity, Bernoulli’s theorem and Poiseuille’s law. Here we are given the difference in the height of the two water columns. We can use the first equation of continuity to find the relationship between the incoming and outgoing velocity and then can apply Bernoulli’s theorem to arrive at a meaningful solution.

Complete step by step answer:
From equation of continuity, \[{{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}\]
Given,
${{A}_{1}}=4\times {{10}^{4}}{{m}^{2}} \\ $
${{A}_{2}}=2\times {{10}^{4}}{{m}^{2}} \\ $
$\Rightarrow {{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}} \\ $
$\Rightarrow 4\times {{10}^{4}}\times {{v}_{1}}=2\times {{10}^{4}}\times {{v}_{2}} \\ $
$\therefore 2{{v}_{1}}={{v}_{2}} \\ $
Now, from Bernoulli’s theorem: \[{{P}_{1}}+\dfrac{\rho v_{1}^{2}}{2}+\rho g{{h}_{1}}={{P}_{2}}+\dfrac{\rho v_{2}^{2}}{2}+\rho g{{h}_{2}}\]
We can see from the figure given in the question that both column A and B are at same height, \[{{h}_{2}}={{h}_{1}}\]
$ \Rightarrow {{P}_{1}}+\dfrac{\rho v_{1}^{2}}{2}+\rho g{{h}_{1}}={{P}_{2}}+\dfrac{\rho v_{2}^{2}}{2}+\rho g{{h}_{2}} \\
\Rightarrow {{P}_{1}}-{{P}_{2}}=\dfrac{\rho v_{2}^{2}}{2}-\dfrac{\rho v_{1}^{2}}{2} \\
\Rightarrow {{P}_{1}}-{{P}_{2}}=\dfrac{\rho }{2}(v_{2}^{2}-v_{1}^{2}) \\
\Rightarrow {{P}_{1}}-{{P}_{2}}=\dfrac{\rho }{2}(4v_{1}^{2}-v_{1}^{2}) \\
 \Rightarrow {{P}_{1}}-{{P}_{2}}=\dfrac{\rho }{2}(3v_{1}^{2}) \\ $
Both the air column given, the difference of heights of water column in the vertical tubes is h=0.02m, so,
\[{{p}_{1}}={{p}_{2}}=2\times 1\times 1000dyn/c{{m}^{2}}\]
\[\therefore {{v}_{1}}=\sqrt{\dfrac{4000}{3}}=36.51cm/s\]
So, the rate of flow is \[{{v}_{1}}{{A}_{1}}=36.51\times 4=146c{{m}^{3}}/s\]

So, the correct answer is “Option B”.

Note:
Bernoulli's theorem is based upon the law of conservation of energy. In fact, mechanical energy and this theorem does not hold if the liquid is compressible. Equation of continuity holds for streamline flow and for incompressible fluid. All the units must be taken in standard SI, but the answer was given in cm so we have changed the units accordingly as per our comfort.