Question

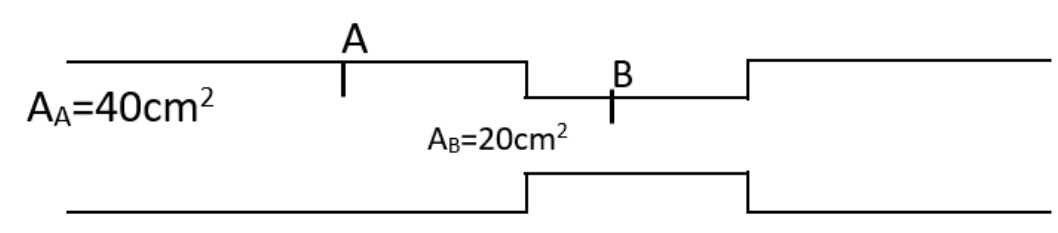
Water flows in a horizontal tube as shown in the figure. The pressure of water changes by $700N{{m}^{2}}$ between A and B where the area of the cross-section is $40c{{m}^{2}}$ and $20c{{m}^{2}}$, respectively. Calculate the rate of flow of water through the tube. (Density of water $=1000kg{{m}^{3}}$)

$\begin{align}
  & A.3020c{{m}^{3}}/s \\
 & B.2420c{{m}^{3}}/s \\
 & C.2720c{{m}^{3}}/s \\
 & D.1810c{{m}^{3}}/s \\
\end{align}$

Answer 1

Hint: Firstly the continuity equation is to be used here. The equation says that the product of the area of the surface and the velocity when it enters a pipe will be equivalent to the same when it is leaving the pipe. After obtaining the results, Bernoulli's equation is used to find the flow rate.
Formula used:
${{P}_{A}}+\dfrac{1}{2}\rho {{V}_{A}}^{2}={{P}_{B}}+\dfrac{1}{2}\rho {{V}_{B}}^{2}$

Complete step-by-step solution:
The changes in the pressure is mentioned in the question as,
$\Delta P=700N{{m}^{-2}}$
The area of cross-section of the position marked A is given as,
${{A}_{B}}=20c{{m}^{2}}$
And the area of cross section of the position marked as B is given as,
${{A}_{B}}=20c{{m}^{2}}$
According to the continuity equation, we can write that,
${{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}}$
Where ${{V}_{A}}$ and ${{V}_{B}}$are the velocities at the A and B positions respectively,
Substituting the values of areas in the equation will be given as,
$\begin{align}
  & 40\times {{V}_{A}}=20\times {{V}_{B}} \\
 & \Rightarrow 2{{V}_{A}}={{V}_{B}} \\
\end{align}$
Now let us use the Bernoulli’s equation, which tells that,
${{P}_{A}}+\dfrac{1}{2}\rho {{V}_{A}}^{2}={{P}_{B}}+\dfrac{1}{2}\rho {{V}_{B}}^{2}$
Where ${{P}_{A}}$ and ${{P}_{B}}$ are the pressure inside the pipe at A and B positions respectively. Density of water is mentioned in the question. And also note that the vertical height is the same here. That is why the height term is not used.
Rearranging the equation will give,
${{P}_{A}}-{{P}_{B}}=\dfrac{1}{2}\rho \left( {{V}_{B}}^{2}-{{V}_{A}}^{2} \right)$
Where we all know,
${{P}_{A}}-{{P}_{B}}=\Delta P$
Substituting the values in it,
\[\begin{align}
  & \Delta P=\dfrac{1}{2}\times {{10}^{3}}\left( {{\left[ 2{{V}_{A}} \right]}^{2}}-{{V}_{A}}^{2} \right) \\
 & \Rightarrow \Delta P=\dfrac{1}{2}\times {{10}^{3}}\left( 4{{V}_{A}}^{2}-{{V}_{A}}^{2} \right) \\
\end{align}\]
Simplifying this equation will give,
\[\Delta P=\dfrac{3}{2}{{V}_{A}}^{2}\times {{10}^{3}}\]
Now let us substitute the values in it,
\[700=\dfrac{3}{2}{{V}_{A}}^{2}\times {{10}^{3}}\]
Rearranging the equation will give,
\[{{V}_{A}}^{2}=\dfrac{700\times 2}{3\times {{10}^{3}}}=\dfrac{7}{15}{{m}^{2}}{{s}^{-2}}\]
Taking the square root will give,
\[{{V}_{A}}=\sqrt{\dfrac{7}{15}}m{{s}^{-1}}=\sqrt{\dfrac{7}{15}}\times 100cm{{s}^{-1}}\]
Therefore the flow rate at A is given as,
\[vol={{A}_{A}}\times {{V}_{A}}\]
Substituting the values in it,
\[vol=40\times \sqrt{\dfrac{7}{15}}\times 100c{{m}^{3}}{{s}^{-1}}\]
Simplifying this equation will give,
\[vol=40\times 0.68313\times 100c{{m}^{3}}{{s}^{-1}}\]
That is,
\[\begin{align}
  & vol=40\times 68.313c{{m}^{3}}{{s}^{-1}} \\
 &\Rightarrow vol=2732.52c{{m}^{3}}{{s}^{-1}} \\
\end{align}\]
As per the options, the flow rate at B can be approximated as,
\[vol=2732.52c{{m}^{3}}{{s}^{-1}}\approx 2720c{{m}^{3}}{{s}^{-1}}\]
Therefore the option C is correct.

Note: Bernoulli's principle is having a great role in fluid dynamics. This law states that an increase in the speed of fluid happens in accordance with a decrease in static pressure or a decrease in the potential energy of the fluid. That is the sum of kinetic energy, pressure energy, and the potential energy per unit mass of a non-viscous, incompressible fluid in a streamlined flow is fixed.