Question

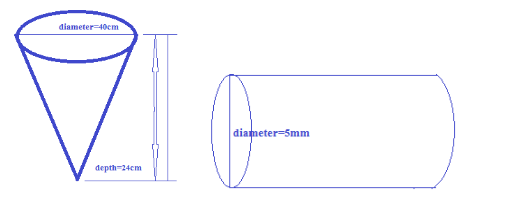
Water flows at the rate of 10 m per minute through a cylindrical pipe having its diameter as 5 mm. How much time will it take to fill a conical vessel whose diameter of the base is 40 cm and depth 24 cm?
A.51.2
B.50.2
C.45.2
D.49.2

Answer 1

Hint: We have given the diameter of cylinder Base diameter of cone and depth of cone. They all do not have the same unit. Firstly we have to convert all the quantities in the same unit. Then we calculate the volume of the cone. Now we have to give the lengths of the cylinders. We have speed of flow of water. We consider the time taken by the water to fill the tank and with the help of the speed of time variable we calculate the length of the tank. In the end we equate the volume of the cone and the volume of the cylinder as their volumes are the same. This unit helps in finding the time.

Complete step by step solution:
Given that,
Diameter of cone = \[40cm\]
Radius of cone = \[\dfrac{1}{2}Diameter\] = \[\dfrac{1}{2} \times 40 = 20cm\]
Depth of cone = \[24cm\]

Volume of cone = \[\dfrac{1}{3}\pi {r^2}h\]
Putting the values we get,
 \[{V_{cone}} = \dfrac{1}{3}\pi \times {\left( {20} \right)^2} \times 24\] …………………..I
Now diameter of cylinder = \[5mm\]
But since the dimensions are in cm we will convert it into cm.
Now we know that \[1mm = \dfrac{1}{{10}}cm\]
So \[5mm = \dfrac{5}{{10}} = 0.5cm\]
Radius of cylinder= \[\dfrac{1}{2}Diameter\] = \[\dfrac{1}{2} \times 0.5 = 0.25cm\]
Let \[l\] be length of cylinder

Volume of the cylinder = \[\pi {r^2}l\]

Putting the values we get,

 \[{V_{cylinder}} = \pi \times {\left( {0.25} \right)^2} \times l\] …………………..II
We have given that speed of flow is \[10m/\min \]
But all other dimensions are in cm. so above rate of flow is given by,
= \[10 \times 100m/\min = 1000cm/\min \]
Let be the time taken by water to fill the tank.
Now \[l = 1000 \times t\]
because the rate of flow is the length of the cylinder itself. Now putting this value of l in equation of volume of cylinder we get,
 \[{V_{cylinder}} = \pi \times {\left( {0.25} \right)^2} \times 1000t\]
 Now we know that the volume of water flowing from the cylindrical vessel is equal to the volume of water filling in the cone. So equating this we get,
 \[\pi \times {\left( {0.25} \right)^2} \times 1000t = \dfrac{1}{3}\pi \times {\left( {20} \right)^2} \times 24\]
Cancelling \[\pi \] we get,
 \[{\left( {0.25} \right)^2} \times 1000t = \dfrac{1}{3} \times {\left( {20} \right)^2} \times 24\]
Taking the squares of the numbers so mentioned,
 \[0.0625 \times 1000t = \dfrac{1}{3} \times 400 \times 24\]
On solving the terms we get,
 \[62.5t = 400 \times 8\]
Multiplying both sides by 10 we get,
 \[625t = 4000 \times 8\]
Now to find the value of t we are rearranging the terms,
 \[t = \dfrac{{4000 \times 8}}{{625}}\]
Dividing by 25 we get,
 \[t = \dfrac{{160 \times 8}}{{25}}\]
On simplifying further,
 \[t = 6.4 \times 8\]
On taking the product we get,
 \[t = 51.2\]
This is the answer that is time taken to fill the conical flask.
Option (A) is correct
So, the correct answer is “Option A”.

Note: Volume:
Volume is the quantity of three dimensions of space enclosed by the closed surface. Example the space that a substance occupies volume is often qualified numerically using the SI derived units.
Volume of cone is \[\dfrac{1}{3}\pi {r^2}h\] and volume of cylinder is \[\pi {r^2}l\] .
Note that the water emptied from a cylindrical pipe is equal to the water stored in a conical vessel. This is the important factor that decides the way of answer.