Question

Water drops are falling in regular intervals of time from the top of tower of height \[9\,{\text{m}}\]. If the 4th drop begins to fall when the 1st drop reaches the ground, find the positions of the 2nd and 3rd drops from the top of the tower.

Answer 1

Hint:Use the kinematic equation for displacement of an object. Using this kinematic equation determines the time required for the first drop to reach the ground. Then divide this time by 3 to determine the time lag between the three drops as the fourth drop begins to fall when the first drop reaches the ground. Using this time lag, determine the times and determine the positions of the second and drops when the first drop reaches the ground using a kinematic equation.

Formula used:
The kinematic equation for displacement \[s\] of an object is given by
\[s = ut + \dfrac{1}{2}a{t^2}\] …… (1)
Here, \[u\] is initial velocity of the object, \[t\] is the time and \[a\] is acceleration of the object.

Complete step by step answer:
We have given that the height of the tower is \[9\,{\text{m}}\].
\[H = 9\,{\text{m}}\]
The water drops are falling at regular intervals from top of the tower. Also when the 1st drop reaches the ground, the 4th drop begins to fall.
Initial velocity of all the drops is zero.
Hence, the equation (1) becomes
\[s = \dfrac{1}{2}g{t^2}\] …… (2)
Let us first determine the time at which the first drop reaches the ground.
Rewrite equation (2) for the displacement of the first drop.
\[H = \dfrac{1}{2}g{t^2}\]
Substitute \[9\,{\text{m}}\] for \[H\] and \[9.8\,{\text{m/}}{{\text{s}}^{\text{2}}}\] for \[g\] in the above equation.
\[\left( {9\,{\text{m}}} \right) = \dfrac{1}{2}\left( {9.8\,{\text{m/}}{{\text{s}}^{\text{2}}}} \right){t^2}\]
\[ \Rightarrow t = \sqrt {\dfrac{{18}}{{9.8}}} \]
\[ \Rightarrow t = 1.355\,{\text{s}}\]
Hence, the time required for the first drop to reach the ground is \[1.355\,{\text{s}}\].
At this time the fourth drop begins to drop from the top of the tower.This shows that when the first drop reaches the ground, second and third drop are in the path of their motion.As the drops are falling from the tower in an equal interval of times, this time and displacement of the first three drops is divided equally for three drops.Thus, the time lag between the three drops can be determined as
\[\dfrac{{1.355\,{\text{s}}}}{3} = 0.45\,{\text{s}}\]
Thus, the time lag between the first three drops is \[0.45\,{\text{s}}\].

The diagram representing the positions of the first four drops is as follows:

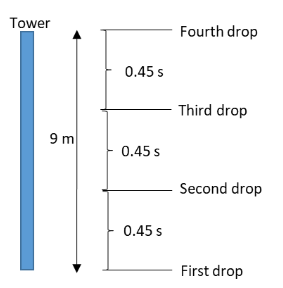
From the above diagram, we can conclude that we need to determine the positions of the second and third drop from the top of the tower at times \[0.45\,{\text{s}}\] and \[0.9\,{\text{s}}\] respectively.Substitute \[9.8\,{\text{m/}}{{\text{s}}^{\text{2}}}\] for \[g\] and \[0.45\,{\text{s}}\] for \[t\] in the equation (2).
\[s = \dfrac{1}{2}\left( {9.8\,{\text{m/}}{{\text{s}}^{\text{2}}}} \right){\left( {0.45\,{\text{s}}} \right)^2}\]
\[ \Rightarrow s = 0.9922\,{\text{m}}\]
Thus, the position of the third drop from the top of the tower is \[0.9922\,{\text{m}}\].
Substitute \[9.8\,{\text{m/}}{{\text{s}}^{\text{2}}}\] for \[g\] and \[0.9\,{\text{s}}\] for \[t\] in the equation (2).
\[s = \dfrac{1}{2}\left( {9.8\,{\text{m/}}{{\text{s}}^{\text{2}}}} \right){\left( {0.9\,{\text{s}}} \right)^2}\]
\[ \therefore s = 3.969\,{\text{m}}\]
Thus, the position of the second drop from the top of the tower is \[3.969\,{\text{m}}\].

Hence, the 2nd and 3rd drops when the 1st drop reaches the ground are at positions \[3.969\,{\text{m}}\] and \[0.9922\,{\text{m}}\] from the top of the tower.

Note:The students should correctly determine the time of the second and third drop when the first drop reaches the ground. Also the students should keep in mind that we need to divide the time required to reach the first drop to the ground by 3 and not 4 as the fourth drop at this time has not started its free falling motion.