Question

Water and oil are poured into the two limbs of a U-tube containing mercury. The interfaces of the mercury and the liquids are at the same height in both limbs. Determine the height of the water column $h_1$ if that of the oil $h_2=20\;cm$. The density of the oil is$\;0.9$.

Answer 1

Hint: Recall that Pascal’s principle suggests an equal and undiminished transmission of pressure throughout all points of an enclosed incompressible fluid. In such a case, pressure exerted on one arm of mercury will be transmitted entirely to the other arm of mercury. We know that the pressure on the arms of mercury arise from the atmospheric pressure as well as the fluid pressure of water and oil. Use the above deductions to arrive at an equation to solve for the height of the water column.

Formula Used:
Absolute pressure $P_{abs} = P_0 + P_{fluid}$
Gauge pressure $P_{fluid} = \rho gh$

Complete step-by-step solution:
Let us begin by understanding Pascal’s Law, which we will employ in order to evaluate the problem given to us.
Pascal’s Law is a fluid mechanical principle that describes that transmission of pressure through a fluid. It states that a pressure change at any point in a confined incompressible fluid will be transmitted throughout the fluid such that the same change occurs everywhere. What this means for the U-tube is that, the pressure exerted on the left arm of the U-tube containing mercury by the water will transmit the same amount of pressure throughout the mercury into the right arm of the U-tube against the oil or vice versa. In any case, the pressure experienced by both arms of the mercury will be equal, i.e.,
$P_{left\;arm} = P_{right\;arm}$

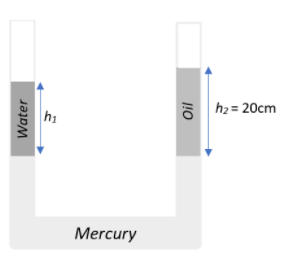
Given that the height of the water and oil columns are $h_{1}$, and $h_2 = 20\;cm$ respectively. Let the acceleration due to gravity be$\;g$ and let the density of water be $\rho_{water}=1$ and that of oil is given to be $\rho_{oil} = 0.9$
The pressure on each arm of mercury arises from the atmospheric pressure $P_0$ as well as the fluid pressure exerted by water and oil on the mercury respectively, i.e.,
$P_0 + P_{water} = P_{0} + P_{oil}$
$\Rightarrow P_{water} = P_{oil}$
$\Rightarrow \rho_{water}gh_1 = \rho_{oil}gh_2$
$\Rightarrow h_1 = \dfrac{\rho_{oil} \times h_2}{\rho_{water}} = \dfrac{0.9 \times 20}{1} = 18\;cm$
Therefore the height of the water column is found to be $18\;cm$.

Note: It is important to note that the intuitive interpretation of Pascal’s Law and its relation to fluid or hydrostatic pressure is that the difference in pressure between the two arms of different fluid in a tube is due to the difference in weight exerted by the fluids. It thus becomes crucial to account for ambient atmospheric pressure and well as hydrostatic pressure where both vary with height, while doing any calculations that pertain to Pascal’s Law and transmission of pressure.