Question

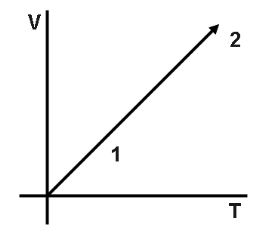
Volume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process 1−2 is.

A. $3$
B. $\dfrac{5}{2}$
C. $\dfrac{5}{3}$
D. $\dfrac{7}{2}$

Answer 1

Hint:To solve this question, we will directly use the specific heat at a constant pressure of monatomic gas and substitute the same value in the equation of heat absorbed. Then we will simply divide the equation with the equation of the work done in the case of the isobaric process to get the required solution

Formula used:
$\vartriangle U = n{C_v}\vartriangle T$
$\Rightarrow \vartriangle Q = n{C_p}\vartriangle T$
Where, $n$ is the number of moles, ${C_p}$ is the heat at constant pressure, ${C_v}$ is the molar heat capacity and $\vartriangle T$ is the change in temperature.

Complete step by step answer:
Since, $V \propto T$ is a straight line. Therefore, we can say that, $P$ is constant. And here it is given, $n = 2$ and $He$ is a monatomic gas.
As $\vartriangle Q = n{C_p}\vartriangle T$ ,
$\vartriangle U = n{C_v}\vartriangle T$
Also,
$\vartriangle W = \vartriangle Q - \vartriangle U \\
\Rightarrow \vartriangle W = \mu ({C_p} - {C_v})\vartriangle T \\ $
Therefore, required ratio is,
$\dfrac{{\vartriangle Q}}{{\vartriangle W}} = \dfrac{{n{C_p}\vartriangle T}}{{n({C_p} - {C_v})\vartriangle T}} \\
\Rightarrow \dfrac{{\vartriangle Q}}{{\vartriangle W}} = \dfrac{{{C_p}}}{{{C_p} - {C_v}}} \\ $
Further we can write,
\[\dfrac{{\vartriangle Q}}{{\vartriangle W}} = \dfrac{{{C_p}}}{{{C_p} - {C_v}}} \\
\Rightarrow \dfrac{{\vartriangle Q}}{{\vartriangle W}} = \dfrac{1}{{1 - \dfrac{{{C_v}}}{{{C_p}}}}} \\ \]
And we know that for monoatomic gas $\gamma = \dfrac{{{C_p}}}{{{C_v}}} = \dfrac{5}{3}$. Now, substituting the value in above equation,
\[\dfrac{{\vartriangle Q}}{{\vartriangle W}} = \dfrac{1}{{1 - \dfrac{{{C_v}}}{{{C_p}}}}} \\
\Rightarrow \dfrac{{\vartriangle Q}}{{\vartriangle W}} = \dfrac{1}{{1 - \dfrac{3}{5}}} \\
\therefore \dfrac{{\vartriangle Q}}{{\vartriangle W}} = \dfrac{5}{2} \]
Therefore, the ratio of the heat absorbed and the work done by the gas from process 1-2 is: \[\dfrac{5}{2}\] .

Hence, the correct option is B.

Note:Note that, in the graph of volume versus temperature every line describes the isobar, which means the atoms which have the same mass number and different atomic number. The graph also represents Charles’s law. And the graph which is plotted shows constant pressure.