Question

How is the volume of the cylinder affected when its radius is doubled?

Answer 1

Hint: A cylinder can be defined as a closed solid having parallel circular bases attached by a curved surface. It is a three- dimensional shape with two circular ends called bases which are parallel to each other. The volume of the cylinder is given by the formula $\pi {r^2}h$ where $r$ is the radius of the cylinder and $h$ is the height of the cylinder. Here, in this question we have asked the affect on the volume of cylinder when its radius is doubled so we take the ratio of the volumes and simplify it.

Complete step by step answer:
A cylinder can be defined as a closed solid having parallel circular bases attached by a curved surface. It is a three- dimensional shape with two circular ends called bases which are parallel to each other and the surface that connects the two circular ends is basically a rectangle. In cylinder radius is the line segment extending from the centre of its curved surface to the circumference of its bounding surface and height is the perpendicular distance between two circular surfaces.

A cylinder can be a hollow or a solid. A hollow cylinder is empty from inside whereas a solid cylinder is packed with some material. The volume of a cylinder can be defined as the space occupied by a cylinder. For a hollow cylinder, it is the space enclosed inside a cylinder and for a solid cylinder it is the amount of material it is made of. The volume of the cylinder is equal to the product of area of circular base into height of the cylinder. Therefore, the above statement can be written as,
$V = \pi {r^2}h$
Where $r$ is the radius of the cylinder and $h$ is the height of the cylinder.

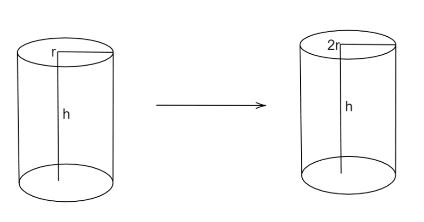
According to the above figure the radius of the cylinder is doubled.
So, let’s assume ${V_1}$ be the volume of the cylinder with radius ${r_1} = r$ and ${V_2}$ be the volume of the cylinder with radius ${r_2} = 2r$
Volume of the cylinder is given by $V = \pi {r^2}h$
Therefore, $V \propto {r^2}$
Removing the proportionality constant. We get,
$ \Rightarrow V = k{r^2}$
So, ${V_1} = k{r^2}$ and ${V_2} = k{(2r)^2}$
On dividing ${V_2}$by ${V_1}$. We get,
$ \Rightarrow \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{k{{(2r)}^2}}}{{k{r^2}}}$
Cancelling out the equal terms. We get,
$\therefore \dfrac{{{V_2}}}{{{V_1}}} = 4$
Therefore, ${V_2} = 4{V_1}$

Hence, when the radius of the cylinder is doubled its volume quadrupled.

Note: In cylinder the two circular bases are always parallel and congruent to each other. When the axis forms a right angle with the bases of the cylinder which are opposite to each then the cylinder would be considered a right cylinder. The cylinders which have circular bases are called circular cylinders whereas cylinders having elliptical bases are known as Elliptical cylinders.