Question

What is the volume of a right cylinder with radius \[3\]cm and height \[5\]cm?

Answer 1

Hint: The cylinder is a three-dimensional solid, whose circular base & top are parallel to each other. The perpendicular distance between the top and the base is known as the total height of the cylinder.
The curved surface area is defined as the area of the only curved surface, leaving the circular top & base.
Formula:
If we take the height of the cylinder h and base radius r,
The curved surface area of the cylinder is \[2\pi rh\]
The volume of the cylinder is =\[\pi {r^2}h\]

Complete step by step answer:
It is given that; the right cylinder has radius \[3\]cm and height \[5\] cm.

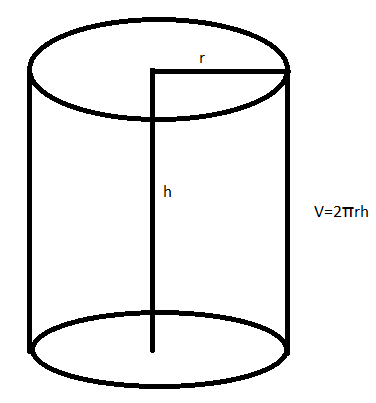
Here, height h= \[5\]cm
Radius =r =\[3\]cm
The volume of the cylinder is \[\pi {r^2}h\]
Putting the values of r and h we get,
The volume of the cylinder is
\[
  \pi {r^2}h \\
   = \dfrac{{22}}{7} \times {3^2} \times 5 \\
   = \dfrac{{22}}{7} \times 9 \times 5 \\
   = 141.428571c{m^3} \\
\ \]
\[ \simeq 141.43c{m^3}\]
The volume of the cylinder is \[141.43c{m^3}\]

Note: A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes which consist of a circular base and a height. It is the idealized version of a solid physical tin that can have lids on top and bottom.
If the base of a circular cylinder has a radius r and the cylinder has height h, then the volume is given by,
If the axis is vertical, the surface area of a right circular cylinder consists of three parts.
The area of the top base: \[\pi {r^2}\]
The area of the bottom base: \[\pi {r^2}\]
The area of the side: \[2\pi rh\]
Therefore we get, the surface area of a cylinder is\[2\pi rh + 2\pi {r^2} = 2\pi r(h + r)\].