Question

Volume of a hollow sphere is $ \dfrac{11352}{7}\text{ cm}^{3} $ . If the outer radius is 8 cm, find the inner radius of the sphere. (Take $ \pi =\dfrac{22}{7} $ )

Answer 1

Hint: A sphere is a ball-shaped three-dimensional object.
The volume of a sphere of radius r units is $ \dfrac{4}{3}\pi {{r}^{3}} $ cubic units.
The volume of the material used in making a hollow sphere = Volume of outer sphere - Volume of inner sphere.
Assume the inner radius to be x cm, form an equation and solve.

Complete step by step answer:
Let's say that the inside radius of the hollow sphere is x cm and the outside radius is $ y=8\text{ cm} $ .

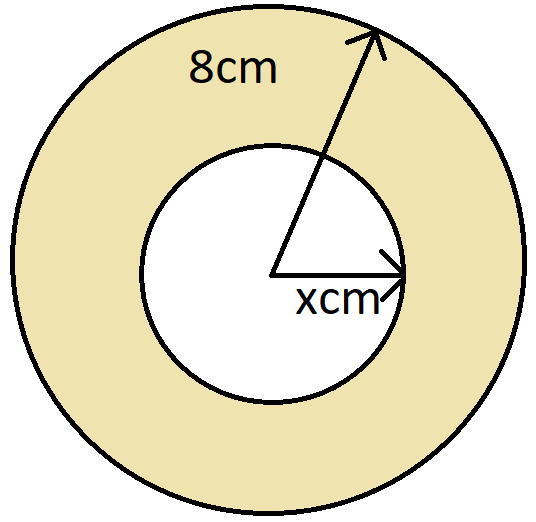
Using the formula $ V=\dfrac{4}{3}\pi {{r}^{3}} $ , the volume of the outside sphere is $ \dfrac{4}{3}\pi {{8}^{3}} $ and the volume of the inside sphere is $ \dfrac{4}{3}\pi {{x}^{3}} $ .
The volume of the hollow sphere (shaded part) will be $ \dfrac{4}{3}\pi {{8}^{3}}-\dfrac{4}{3}\pi {{x}^{3}} $ .
According to the question:
 $ \dfrac{4}{3}\pi {{8}^{3}}-\dfrac{4}{3}\pi {{x}^{3}}=\dfrac{11352}{7} $
Taking out the common factors $ \dfrac{4}{3}\pi $ and using $ \pi =\dfrac{22}{7} $ , we get:
⇒ $ \dfrac{4}{3}\times \dfrac{22}{7}\times \left( {{8}^{3}}-{{x}^{3}} \right)=\dfrac{11352}{7} $
⇒ $ {{8}^{3}}-{{x}^{3}}=\dfrac{11352}{7}\times \dfrac{7}{22}\times \dfrac{3}{4} $
Note that 11352 is multiple of 11, because $ (1+3+2)-(1+5)=6-6=0 $ . Dividing 11352 by 22 and cancelling out the 7's, we get:
⇒ $ 512-{{x}^{3}}=516\times \dfrac{3}{4} $
⇒ $ 512-{{x}^{3}}=129\times 3 $
⇒ $ 512-{{x}^{3}}=387 $
⇒ $ {{x}^{3}}=512-387 $
⇒ $ {{x}^{3}}=125 $
Since, $ 5\times 5\times 5=125 $ , we get:
⇒ $ x=5 $

∴ The inner radius of the sphere is 5 cm.

Note: The same idea can be applied to solids of other shapes. The surface area of a sphere is $ 4\pi {{r}^{2}} $ sq. units. The half of a sphere is also called a hemi-sphere.