Question

Volume of a cuboid with x as length, $y$ as breadth and \[z\] as height is?

Answer 1

Hint: Let us first define the volume; which is the amount of the space that will be occupied by the three-dimensional figure as it's measured in the cubic units.
Length is the measurement that something objects from end to end, or also known as the measurement of the distance.
Breadth is the distance or like measurements from the given side by side of the objects also the wide range or the extent.
Height is also more likely to the measurements of the objects but from head to foot or else like from the base to the top.

Complete step-by-step solution:
Since the question asks us to find the Volume of a cuboid with x as length and$y$ as the breadth and\[z\] as height.

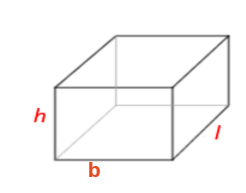
Let the volume of the cuboid formula is $l \times b \times h$.
Thus, we can replace the length as x (as per the given), also we are able to replace the breadth as $y$ (from given), and finally, we are also able to replace the height as \[z\] (from the given).
Thus, replacing the values into the formulas, we get; $l = x$ (length of the cuboid), $b = y$(breadth of the cuboid), and $h = z$(height of the cuboid).
Hence substituting the values into the volume of the cuboid formula we get; $l \times b \times h \Rightarrow x \times y \times z$
Therefore, the volume of the cuboid is $xyz$ (represents the length, breadth, and height).

Note: Since volume can be measured as the inches or quarts or centimeters by the representations of the length, height, and breadth.
The amount of the volume substance will be occupying a particular volume only.
A cuboid is a three-dimensional shape; it has six faces like a square has four faces.