Question

Vertices of an ellipse are \[\left( 0,\pm 10 \right)\] and its eccentricity is \[e=\dfrac{4}{5}\] then the equation of ellipse is
(a) \[90{{x}^{2}}-40{{y}^{2}}=3600\]
(b) \[80{{x}^{2}}+50{{y}^{2}}=4000\]
(c) \[36{{x}^{2}}+100{{y}^{2}}=3600\]
(d) \[100{{x}^{2}}+36{{y}^{2}}=3600\]

Answer 1

Hint: We solve this problem by using the standard equation of the ellipse because the given vertices of the ellipse lie on the Y-axis. The rough figure of the ellipse is shown below.

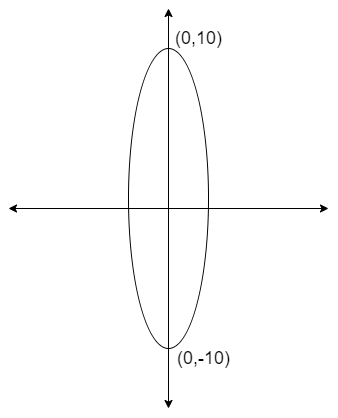
The standard equation of ellipse having the co – ordinate axes as major and minor axis is \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] where \[{{a}^{2}}={{b}^{2}}\left( 1-{{e}^{2}} \right)\]
The above equation has vertices as \[\left( 0,\pm b \right)\] because the major axis is the Y-axis.
By using the above equation we take the vertices of the ellipse to find the values of \[a,b\]


Complete step-by-step solution
We are given that the vertices of ellipse are \[\left( 0,\pm 10 \right)\]
We are also given that the eccentricity of ellipse as \[e=\dfrac{4}{5}\]
Let us assume that the equation of ellipse having the co – ordinate axes as major and minor axes of ellipse as
\[\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]
We know that the vertices of above equation of ellipse are \[\left( 0,\pm b \right)\]
Now, by comparing the above vertices with given vertices we get
\[\Rightarrow b=10\]
Now, let us find the value of \['a'\]
We know that for the standard equation of ellipse we have
\[{{a}^{2}}={{b}^{2}}\left( 1-{{e}^{2}} \right)\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow {{a}^{2}}={{\left( 10 \right)}^{2}}\left( 1-{{\left( \dfrac{4}{5} \right)}^{2}} \right) \\
 & \Rightarrow {{a}^{2}}=100\left( 1-\dfrac{16}{25} \right) \\
\end{align}\]
By subtracting the terms inside the brackets using the LCM we get
\[\begin{align}
  & \Rightarrow {{a}^{2}}=100\left( \dfrac{25-16}{25} \right) \\
 & \Rightarrow {{a}^{2}}=4\times 9 \\
 & \Rightarrow {{a}^{2}}=36 \\
\end{align}\]
Now, by substituting the values of \['{{a}^{2}},b'\] in the equation of ellipse we assumed we get
\[\Rightarrow \dfrac{{{x}^{2}}}{36}+\dfrac{{{y}^{2}}}{100}=1\]
No, by adding the terms using the LCM we get
\[\Rightarrow 100{{x}^{2}}+36{{y}^{2}}=3600\]
Therefore, the equation of ellipse having the vertices as \[\left( 0,\pm 10 \right)\] and its eccentricity as \[e=\dfrac{4}{5}\] is given as \[100{{x}^{2}}+36{{y}^{2}}=3600\]
So, option (d) is the correct answer.

Note: Students may make mistakes in taking the equation of the ellipse.
We are given that the vertices are \[\left( 0,\pm 10 \right)\] this means that the major axis of the ellipse is the Y-axis.
So, for the standard equation of ellipse \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] the vertices will be \[\left( 0,\pm b \right)\] not \[\left( \pm a,0 \right)\]
Also the standard equation of ellipse \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] is applicable only when the major axis and minor axis are co – ordinate axes.
These two points need to be taken care of.