Question

How do you verify the identity \[\cot \left( {\dfrac{\pi }{2} - x} \right) = \tan x\]?

Answer 1

Hint: Use the angle sum property of a triangle and definitions of trigonometric ratios with respect to an acute angle in a right angled triangle to deduce the given identity.

Complete step-by-step solution:
Consider a right angled triangle with right angle at \[\angle B\] and \[\angle C = x\].

It is known that the sum of all interior angles of a triangle is \[\pi \] radian.
\[\angle A + \angle B + \angle C = \pi \]

Substitute \[\angle B\] as \[\dfrac{\pi }{2}\] radian and \[\angle C\] as \[x\] radian to obtain the expression for \[\angle A\] as shown below.
\[ \Rightarrow \angle A + \dfrac{\pi }{2} + x = \pi \]
\[ \Rightarrow \angle A = \dfrac{\pi }{2} - x\]

Therefore, the \[\angle A\] can be expressed as \[\left( {\dfrac{\pi }{2} - x} \right)\] radian.
The right triangle with right angle at \[\angle B\], \[\angle C = x\] and so \[\angle A = \dfrac{\pi }{2} - x\] is shown in the figure below.

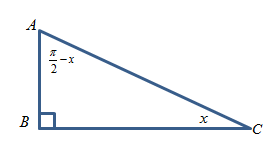
Now, use the definition of trigonometric ratio for \[\tan x\] and \[\cot \left( {\dfrac{\pi }{2} - x} \right)\] to solve further.
For an angle \[x\] as argument, side \[AB\] act as perpendicular (side in front of the argument angle), side \[BC\] act as base and side \[AC\] always be hypotenuse for this triangle.

Therefore, the trigonometry ratio \[\tan x\] defined as the ratio of perpendicular to the base is written as,
\[\tan x = \dfrac{P}{B}\]
\[ \Rightarrow \tan x = \dfrac{{AB}}{{BC}}\] …… (1)

For angle \[\left( {\dfrac{\pi }{2} - x} \right)\] as argument, side \[BC\] act as perpendicular (side in front of the argument angle), side \[AB\] act as base and side \[AC\] always be hypotenuse for this triangle.

Therefore, the trigonometry ratio \[\cot \left( {\dfrac{\pi }{2} - x} \right)\] defined as the ratio of base to the perpendicular is written as,

\[\cot \left( {\dfrac{\pi }{2} - x} \right) = \dfrac{B}{P}\]
\[ \Rightarrow \cot \left( {\dfrac{\pi }{2} - x} \right) = \dfrac{{AB}}{{BC}}\] …… (2)

From the equation (1) and (2), it is verified that \[\cot \left( {\dfrac{\pi }{2} - x} \right) = \tan x\].

Note: Angle \[\dfrac{\pi }{2}\] radian is equivalent to \[90^\circ \] degree. The transformation of angle in degree to angle in radian can be done by the use of relation \[\pi \,rad = 180^\circ \].
There are few other trigonometric identities similar to the given identity.
The relation between sine and cosine ratio in terms of conjugate angles is shown below.
\[ \Rightarrow \sin \left( {\dfrac{\pi }{2} - x} \right) = \cos x\]
\[ \Rightarrow \cos \left( {\dfrac{\pi }{2} - x} \right) = \sin x\]
The relation between cosecant and secant ratio in terms of conjugate angles is shown below.
\[ \Rightarrow \cos ec\left( {\dfrac{\pi }{2} - x} \right) = \sec x\]
\[ \Rightarrow \sec \left( {\dfrac{\pi }{2} - x} \right) = \cos ecx\]