Question

Verify the identity $cos(A-B)=\cos A\cos B+\sin A\sin B$ for $A=B=60{}^\circ $ .

Answer 1

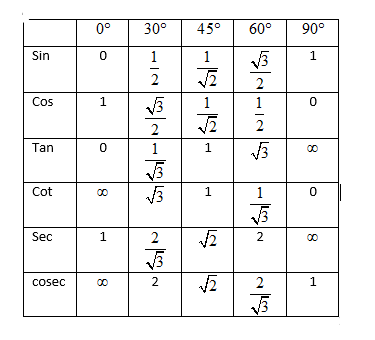
Hint: Start with the LHS of the equation given in the question and put $A=B=60{}^\circ $ . Then use the trigonometric table to put the value of $\cos 0{}^\circ $ , that is one and move to RHS. Use the values $\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}\text{ and cos60}{}^\circ \text{=}\dfrac{1}{2}$ in order to show that RHS is also equal to 1 and verify the identity.

Complete step by step solution:
Before moving to the solution, let us discuss the nature of sine and cosine function, which we would be using in the solution. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

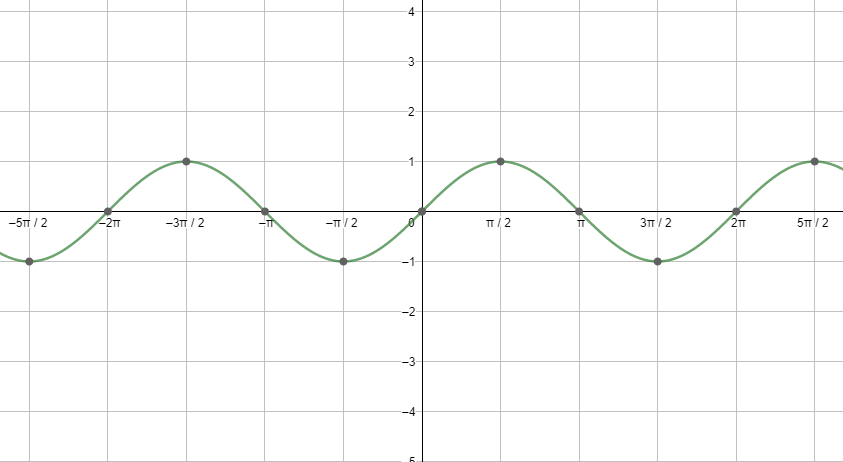
Next, let us see the graph of cosx.

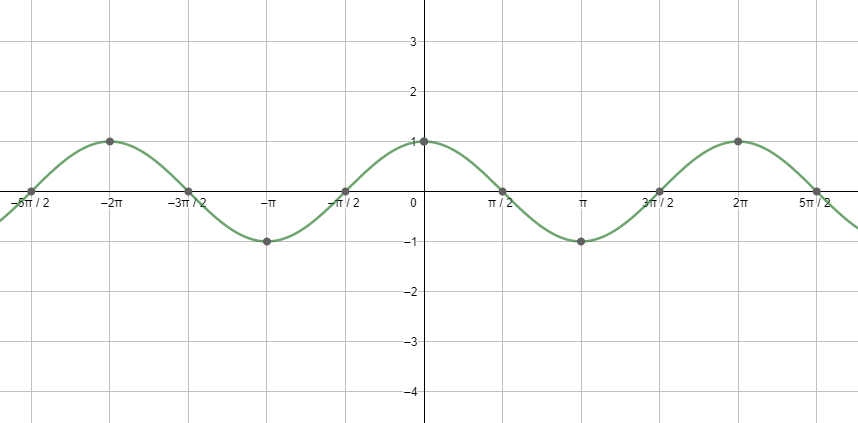
Looking at both the graphs, and using the relations between the different trigonometric ratios, we get

Let us start the solution to the above question by simplifying the left-hand side of the equation $cos(A-B)=\cos A\cos B+\sin A\sin B$ by putting the values $A=60{}^\circ $ and $B=60{}^\circ $ .
$cos(A-B)$
$=\cos (60{}^\circ -60{}^\circ )$
$=\cos 0{}^\circ $
And we know that the value of $\cos 0{}^\circ $ is equal to 1. So, we get
$=\cos 0{}^\circ =1$
So, the left-hand side of the equation $cos(A-B)=\cos A\cos B+\sin A\sin B$ is equal to 1.
Now let us simplify the right-hand side of the equation by putting the values $A=60{}^\circ $ and $B=60{}^\circ $ .
$\cos 60{}^\circ \cos 60{}^\circ +\sin 60{}^\circ \sin 60{}^\circ $
$={{\cos }^{2}}60+{{\sin }^{2}}60{}^\circ $
Now we know that ${{\cos }^{2}}x+{{\sin }^{2}}x=1$ .
${{\cos }^{2}}60+{{\sin }^{2}}60{}^\circ =1$
Therefore, we can say that the left-hand side of the equation $cos(A-B)=\cos A\cos B+\sin A\sin B$ is equal to the right-hand side. So, we have verified the above equation.

Note: It will be very useful if you learn the values of trigonometric ratios for all the standard angles and the properties related to complementary angles and ratios. Also, the formulas and identities related to compound angles are very useful and fundamental as well. Also, don’t get confused between the values $\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}\text{ and cos60}{}^\circ \text{=}\dfrac{1}{2}$ and interchange them, however, in this question interchanging the values may lead to the correct answer but is not true in all the cases.