Question

Verify the Euler’s formula for the given solid.

Answer 1

Hint: Use the Euler’s Formula (i.e. F +V = E + 2), where F is the total number of Faces in the given solid, V is the total number of the vertices and E is the total number of edges. Count all the faces, vertices and the edges, and to verify the Left-Hand side of Euler’s formula equal to the Right-Hand side of the formula.

Complete step by step answer:
We know that the Euler’s formula is given as:
F +V = E + 2 where, F is the total number of Faces in the given solid.
V is the total number of the vertices.
E is the total number of edges.
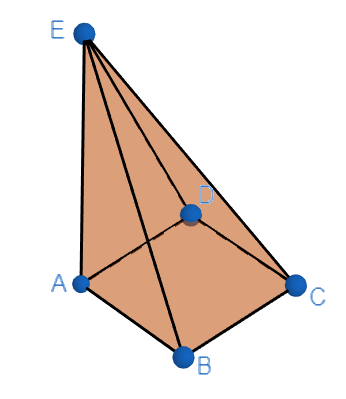
The above given solid is a pyramid whose base is rectangle.
The blue dots in the given figure donates vertices (i.e. corner) of the pyramid.
So, the vertices of the given solid are A, B, C, D, E.
Hence, total number of vertices = 5 = V
Edges of the given solid are AB, BC, CD, AD, DE, AE, BE, CE.
Hence, total number of edges = 8 = E
Now, the faces of the given solid are $\square ABCD,\vartriangle ABE,\vartriangle BCE,\vartriangle CDE,\vartriangle ADE$.
Hence, total number of faces = 5 = F
Now, from Euler’s formula, we know that:
 F +V = E + 2
By putting the value of F, V, E in the above equation, we will get:
\[\Rightarrow 5+5=8+2\]
$\Rightarrow 10=10$
Since, we see that the Left-Hand side of the above equation is equal to the Right-Hand side.
So, Euler’s formula is true for the above given solid.
Hence, verified.

Note: Students usually make mistakes while counting the number of edges, and faces of 3-D figures, because edges and faces usually overlap over each other, when we plot a solid on a plane and they seem to us like they are a single edge or a single face.