Question

How do you verify that parallelogram ABCD with vertices $A\left( -5,-1 \right),$ $B\left( -9,6 \right),$ $C\left( -1,5 \right)$ and $D\left( 3,-2 \right)$ is a rhombus by showing that it is a parallelogram with perpendicular diagonal?

Answer 1

Hint: In order to solve this question first we will find the slope of the parallelogram by using the formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$. If opposite sides are parallel then it is a parallelogram. Then by finding the mid-points we will prove it is the rhombus.

Complete step by step solution:
We have been given the vertices of a parallelogram ABCD with vertices $A\left( -5,-1 \right),$ $B\left( -9,6 \right),$ $C\left( -1,5 \right)$ and $D\left( 3,-2 \right)$.
We have to prove that the parallelogram is a rhombus by showing that it is a parallelogram with perpendicular diagonal.
Let us first draw a diagram of parallelogram ABCD with vertices $A\left( -5,-1 \right),$ $B\left( -9,6 \right),$ $C\left( -1,5 \right)$ and $D\left( 3,-2 \right)$. Then we will get

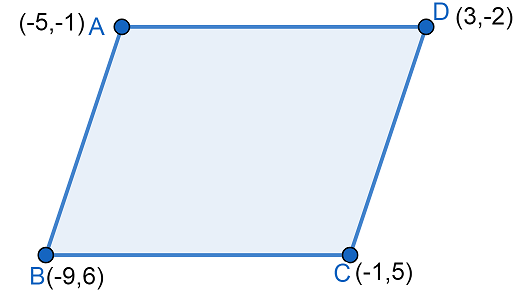
Now, let us find the slope of AB, BC, CD, AD.
Now, we know that the formula of slope is given as $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
Now, the slope of line AB will be
$\Rightarrow {{m}_{AB}}=\dfrac{6-\left( -1 \right)}{-9-\left( -5 \right)}$
Now, solving the above obtained equation we will get
$\begin{align}
  & \Rightarrow {{m}_{AB}}=\dfrac{6+1}{-9+5} \\
 & \Rightarrow {{m}_{AB}}=-\dfrac{7}{4} \\
\end{align}$
Now, the slope of line BC will be
$\Rightarrow {{m}_{BC}}=\dfrac{5-6}{-1-\left( -9 \right)}$
Now, solving the above obtained equation we will get
$\begin{align}
  & \Rightarrow {{m}_{BC}}=\dfrac{-1}{-1+9} \\
 & \Rightarrow {{m}_{BC}}=-\dfrac{1}{8} \\
\end{align}$
Now, the slope of line CD will be
$\Rightarrow {{m}_{CD}}=\dfrac{-2-5}{3-\left( -1 \right)}$
Now, solving the above obtained equation we will get
$\begin{align}
  & \Rightarrow {{m}_{CD}}=\dfrac{-7}{3+1} \\
 & \Rightarrow {{m}_{CD}}= -\dfrac{7}{4} \\
\end{align}$
Now, the slope of line AD will be
$\Rightarrow {{m}_{AD}}=\dfrac{-2-\left( -1 \right)}{3-\left( -5 \right)}$
Now, solving the above obtained equation we will get
$\begin{align}
  & \Rightarrow {{m}_{AD}}=\dfrac{-2+1}{3+5} \\
 & \Rightarrow {{m}_{AD}}=-\dfrac{1}{8} \\
\end{align}$
Now, we get ${{m}_{AB}}={{m}_{CD}}$ and ${{m}_{BC}}={{m}_{AD}}$, so $AB\parallel CD,BC\parallel AD$, ABCD is a parallelogram.
Now, the slope of line AC will be
$\Rightarrow {{m}_{AC}}=\dfrac{5-\left( -1 \right)}{-1-\left( -5 \right)}$
Now, solving the above obtained equation we will get
$\begin{align}
  & \Rightarrow {{m}_{AC}}=\dfrac{5+1}{-1+5} \\
 & \Rightarrow {{m}_{AC}}=\dfrac{6}{4} \\
 & \Rightarrow {{m}_{AC}}=\dfrac{3}{2} \\
\end{align}$
Now, the slope of line BD will be
$\Rightarrow {{m}_{BD}}=\dfrac{6-\left( -2 \right)}{-9-3}$
Now, solving the above obtained equation we will get
$\begin{align}
  & \Rightarrow {{m}_{BD}}=\dfrac{6+2}{-9-3} \\
 & \Rightarrow {{m}_{BD}}=-\dfrac{8}{12} \\
 & \Rightarrow {{m}_{BD}}=-\dfrac{2}{3} \\
\end{align}$
Now, we get ${{m}_{AC}}=-\dfrac{1}{{{m}_{BD}}}$ so, ABCD can be square or a rhombus. Since AB is not perpendicular to AD so it can’t be a square.
Now, we know that if the diagonals bisects each other then it’s a rhombus.
Now, the mid-point of AC and BD will be
$\begin{align}
  & \Rightarrow \text{mid-point of }AC=\dfrac{A\left( -5,-1 \right)+C\left( -1,5 \right)}{2} \\
 & \Rightarrow \text{mid-point of }AC=\left( -3,2 \right) \\
 & \Rightarrow \text{mid-point of BD}=\dfrac{B\left( -9,6 \right)+D\left( 3,-2 \right)}{2} \\
 & \Rightarrow \text{mid-point of BD}=\left( -3,2 \right) \\
\end{align}$
Hence ABCD is a rhombus.

Note: To solve this type of question students must have knowledge of properties of quadrilaterals. A rhombus has opposite sides parallel, opposite angles are equal. The diagonals of a rhombus bisect each other at right angles.