Question

How do you verify $ {\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1 = {\cot ^2}x? $

Answer 1

Hint: We shall solve the above question with the help of one of the three Pythagorean trigonometric identities: $ {\tan ^2}\theta + 1 = {\sec ^2}\theta $ .
Pythagorean identities:
\[
  {\sin ^2}\theta + {\cos ^2}\theta = 1 \\
  1 + {\tan ^2}\theta = {\sec ^2}\theta \\
  1 + {\cot ^2}\theta = {\csc ^2}\theta \;
 \]

Complete step by step solution:
The given question is to verify $ {\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1 = {\cot ^2}x $ .
To prove this, let us first prove the Pythagorean trigonometric identity $ {\tan ^2}\theta + 1 = {\sec ^2}\theta $ .
Consider the below diagram where the point $ (x,y) $ defines an angle $ \theta $ at the origin and $ r $ is the distance from the origin to the point $ (x,y) $ .

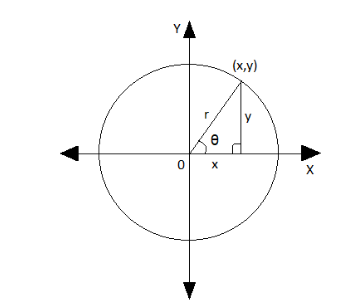
From the above diagram, we can make use of Pythagoras’ theorem to obtain
 $ {y^2} + {x^2} = {r^2} $
Divide throughout by $ {r^2} $ ,
 $ \Rightarrow \dfrac{{{y^2}}}{{{r^2}}} + \dfrac{{{x^2}}}{{{r^2}}} = 1 $
We know that from the diagram,
 $ \dfrac{{{y^2}}}{{{r^2}}} = {\sin ^2}\theta $ and $ \dfrac{{{x^2}}}{{{r^2}}} = {\cos ^2}\theta $
Hence, the expression becomes,
 $ {\sin ^2}\theta + {\cos ^2}\theta = 1 $ , this is an important identity.
Now, let us divide throughout by $ {\cos ^2}\theta $
\[ \Rightarrow \dfrac{{{{\sin }^2}\theta }}{{{{\cos }^2}\theta }} + \dfrac{{{{\cos }^2}\theta }}{{{{\cos }^2}\theta }} = \dfrac{1}{{{{\cos }^2}\theta }}\]
On further simplification we get,
 $ {\tan ^2}\theta + 1 = {\sec ^2}\theta $
Let us replace $ \theta $ by $ \dfrac{\pi }{2} - x $
 $ \Rightarrow {\tan ^2}\left( {\dfrac{\pi }{2} - x} \right) + 1 = {\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) $
Subtracting $ 1 $ from both the sides
 $ \Rightarrow {\tan ^2}\left( {\dfrac{\pi }{2} - x} \right) = {\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1 $
We know that $ \tan \left( {\dfrac{\pi }{2} - \theta } \right) = \cot \theta $
Hence, $ {\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1 = {\cot ^2}x $

Note: Trigonometric identities used in the above solutions are Reciprocal identities, Pythagorean identities and Quotient identities. These identities are given below:
Reciprocal identities:
 $
  \sin \theta = \dfrac{1}{{\csc \theta }} \\
  \cos \theta = \dfrac{1}{{\sec \theta }} \\
  \tan \theta = \dfrac{1}{{\cot \theta }} \;
 $
Pythagorean identities:
\[
  {\sin ^2}\theta + {\cos ^2}\theta = 1 \\
  1 + {\tan ^2}\theta = {\sec ^2}\theta \\
  1 + {\cot ^2}\theta = {\csc ^2}\theta \;
 \]
Quotient identities:
 $
  \dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta \\
  \dfrac{{\cos \theta }}{{\sin \theta }} = \cot \theta \;
 $
There are two more identities other than these. They are Cofunction identities and Even Odd identities.
 $ \bullet $ Learn these formulas that are given above well, so that it will be easier to recognize what procedure and steps are followed in solving such questions.
 $ \bullet $ First, simplify the most complex side so that it has the same form as the simplest side.
That is, first start simplifying on one side and make it look like the other side.
 $ \bullet $ If the given question contains a squared term, then we make use of one of the Pythagorean identities which was mentioned earlier.