Question

Verify Rolle’s theorem for the following function on the indicated interval
$f\left( x \right)={{x}^{2}}+5x+6\text{ on }\left[ -3,-2 \right]$

Answer 1

Hint: Recall the conditions of Rolle’s theorem. Verify whether those conditions are satisfied. If they are satisfied, recall the guarantee of Rolle's theorem. Check whether the guarantee is true for the above function. Hence verify Rolle’s theorem.

Complete step-by-step answer:
Rolle’s theorem: If f(x) is a function such that:
[1] f(x) is continuous in the interval [a,b]
[2] Derivable in the interval (a,b)
[3] f(a) = f(b)
then there exists c such that aHere $f\left( x \right)={{x}^{2}}+5x+6$
Since f(x) is a polynomial and polynomials are continuous for all real x, we have
f(x) is continuous in [-3,-2].
Also f’(x) = 2x+5 is a polynomial in x and hence is continuous in (-3,-2).
Hence f(x) is differentiable in (-3,-2) [Because if the derivative of a function is continuous in an interval, then the function is differentiable in that interval].
Also f(-3) $={{\left( -3 \right)}^{2}}+5\left( -3 \right)+6=9-15+6=0$ and f(-2) $={{\left( -2 \right)}^{2}}+5\left( -2 \right)+6=4-10+6=0$, we have f(-3) = f(-2) = 0.
Hence all conditions of Rolle’s theorem are satisfied. Hence there exists a real number c such that -3 < c < -2 such that
f’(c)=0.
Now f’(c)=2c+5=0
Hence 2c =-5
i.e. $c=-\dfrac{5}{2}$
i.e. c=-2.5.
Now since
-3 <-2.5< -2.
Hence there exists a c = -2.5 such that -3< c < -2 and f’(c) =0.

Note: [1] Rolle’s theorem guarantees the existence of one such “c”, however, does not say anything about the number of such “c”. Hence there may exist more than one such “c” which satisfy the above conditions as in the following graph.

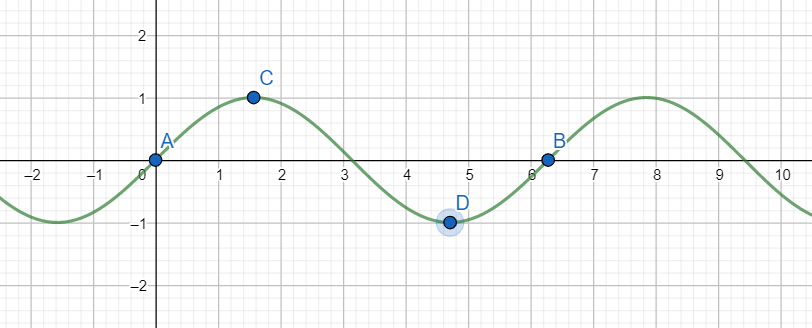
In the interval [A, B] there exist two points C and D at which the derivative of the above function vanishes.