Question

Verify Euler’s form for
A.Square pyramid
B.Triangular prism
C.Rectangular prism

Answer 1

Hint: Euler was a mathematician who discovered the formula for solid three dimensional shapes. That formula includes the vertices, edges and faces of a solid and are calculated in such a way that it satisfies the solid polygon existence.
Formula used:
\[V - E + F = 2\] , where
V→ vertices of the polygon or shape
E →edges of the polygon or shape
F→ faces of the polygon or shape

Complete step-by-step answer:
We will apply this one by one on the given solids.
A.Square pyramid:

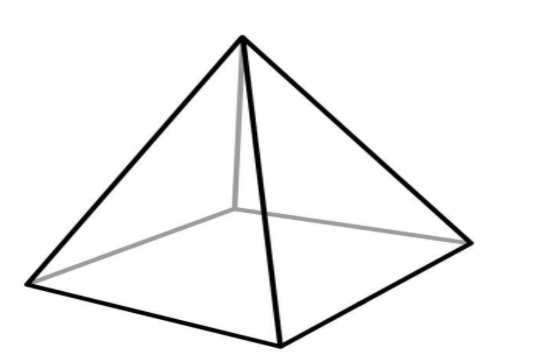
It has vertices V=5 that are 4 from the square base and one of the top pyramid point.
It has edges E=8 that are 4 from the square base and 4 from the pyramid shape.
It has faces F= 5 that is one of the square bases and 4 from the sides of the pyramid.
Now we have all the values of V, E and F. So let’s check for the formula,
\[V - E + F = 2\]
Putting the values as, \[5 - 8 + 5 = - 3 + 5 = 2\]
Thus it holds for square pyramids.

B.Triangular prism:

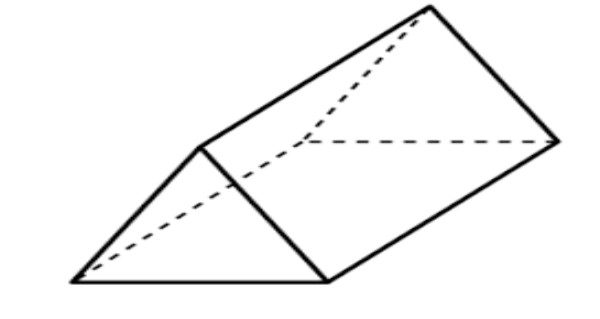
It has vertices V=6 that are 3 from the front triangle and 3 from the rear triangle.
It has edges E=9 that are 3 connecting the front and rear triangle, 3 of front triangle and 3 of rear triangle.
It has faces F= 5 that is 2 of the front and rear triangle and 3 of the body of the prism.
Now we have all the values of V, E and F. So let’s check for the formula,
\[V - E + F = 2\]
Putting the values as, \[6 - 9 + 5 = - 3 + 5 = 2\]
Thus it holds for Triangular prisms.

C.Rectangular prism:

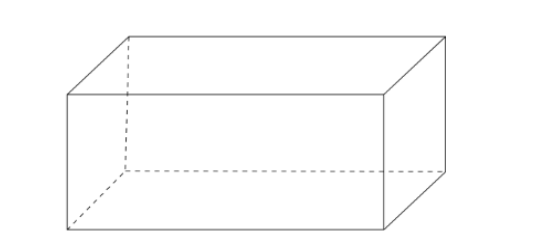
It has vertices V=8 that are 4 from the front rectangle and 4 from the rear rectangle.
It has edges E=12 that are 4 connecting the front and rear rectangle, 4 from the front rectangle and 4 from the rear rectangle.
It has faces F= 6 that are 2 of the front and rear rectangle and 4 of the body of the prism.
Now we have all the values of V, E and F. So let’s check for the formula,
\[V - E + F = 2\]
Putting the values we get, \[8 - 12 + 6 = - 4 + 6 = 2\]
Thus it holds for rectangular prisms.

Note: Note that the concept of prism and pyramid are different. Pyramidal shapes have the base only as the name indicates like triangular pyramid has triangle in base, rectangular pyramid has rectangle in base but they are extended upwards and are joined to a common point at the tip.
Whereas prisms are like front and rear faces are of the shape mentioned and these faces are joined from vertex to vertex.