Question

Velocity-time curve for a body projected vertically upwards is:
A. Parabola
B. Ellipse
C. Hyperbola
D. Straight line

Answer 1

Hint: when a body is projected upwards, its acceleration equals the gravitational acceleration. Since the body is moving in an upward direction, gravitational acceleration will be negative. By equating all these we get the velocity at an instant time,’t’. Compare the obtained equation with the equation of parabola, hyperbola, ellipse and straight line.

Formula used:
Acceleration,
$a=\dfrac{dv}{dt}$
Equation of straight line,
$y=mx+c$

Complete answer:
We have a body which is projected upwards with a velocity ‘v m/s’ in time “t seconds”.
We have to determine the shape of the velocity-time curve so obtained.

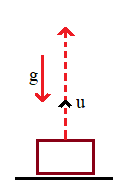
Consider a body which is projected upwards as shown in the above figure.
Its initial velocity, v=u. Since the body is projected in ‘y’ direction, we can say that $v={{u}_{y}}$.
 We know that, when a body is moving upwards the acceleration due to gravity acts downwards.
This acceleration due to gravity will be equal to the acceleration of the body.
‘a = g’, were ‘a’ is the acceleration of the body and ‘g’ is gravitational acceleration.
We know, acceleration is the first derivative of velocity, with respect to time.

$a=\dfrac{dv}{dt}=g$
$\begin{align}
  & \dfrac{dv}{dt}=g \\
 & dv=g\times dt \\
\end{align}$

Now, let us integrate both sides of the equation.

$\int\limits_{u}^{v}{dv=\int\limits_{0}^{t}{gdt}}$ , ‘g’ is a constant.
By integrating, we get,
$\begin{align}
  & v-u=gt \\
 & v=u+gt \\
\end{align}$

We know gravitational acceleration ‘g’, is acting downwards.
Hence ‘g’ is negative.
Therefore we can write the equation $v=u+gt$ as,
$v=u-gt$
Now let us consider the equation of the straight line.
Straight line equation is given as,
$y=mx+c$, where ‘m’ is the slope and ‘c’ is the intercept of y axis.
Now let us compare the straight line equation with the equation we got, i.e. $v=u-gt$ .
From this we can understand that the velocity-time curve of the body projected upwards is a straight line with slope ‘-g’ and y intercept ‘u’.

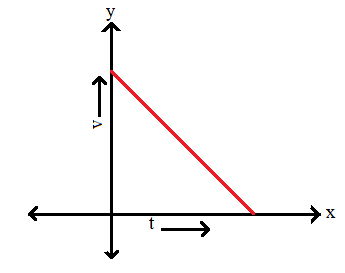
Therefore it is a straight line.

So, the correct answer is “Option D”.

Note:
Velocity of a body is described as the distance or displacement of the body in a particular direction per unit interval of time.
Rate of change in position of a body with respect to time is the average velocity of that body.
Equation of parabola is $y=a{{x}^{2}}+bx+c$
Equation of ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Equation of hyperbola is $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$