Question

Velocity of the center of a small cylinder is v. There is no slipping anywhere. The velocity of the center of the larger cylinder is
\[\begin{align}
  & A.\text{ }2v \\
 & B.\text{ }v \\
 & C.\text{ }\frac{3v}{2} \\
 & D.\text{ None of these} \\
\end{align}\]

Answer 1

Hint: We can find the velocity of the point of contact of the larger cylinder with the floor. That will be the velocity of the center of it as well. Now, to find the velocity of the point of contact, we need to know how much length of the circular surface is being rolled.
Formula used: $ p=2 \pi r $

Complete step-by-step solution:

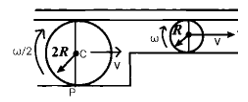
Let us assume that in time T the smaller cylinder has rolled once totally. Then,

$2pR=v.T{{........1}^{st}}$ equation

Now, since there has been no slipping, the distance covered by the smaller cylinder will be the same as the distance covered by the larger one. So, the point of contact of the larger cylinder moves by 2πR along the floor in time T with velocity $v_p$ .

$v_p=\dfrac{2πR}{T}=v$

by using the $1^{st}$ equation.
(Since the larger cylinder has radius 2R, it is not completely rolled once in the time T. It can roll only $\dfrac{2πR}{2π(2R)}=\dfrac{1}{2}$ of its surface in the given time T)
Now, the velocity of the point of contact will be the same as the velocity of the center.

$v_p=v_c$

Hence, the center of the larger cylinder moves by 2πR in time T. Hence its velocity is $v_c=v_p=\dfrac{2πR}{T}=v $ .

Hence option B is the correct answer.

Additional information:
The point of contact of each cylinder with the floor and its center will lie in a straight line which is perpendicular to the floor. This whole line moves with a single velocity.

Note: It’s to be noted that the number of rotations per unit time is different for the two cylinders. The smaller one completes two rations in a time when the larger one completes just one rotation. But this is not to be confused with the velocity of the centers.