Question

Velocity of boat in still water is $13\text{ m/s}$. If water flows in a river with a velocity of $5\text{ m/s}$, what is the difference in times taken by him to cross the river in the shortest path and in the shortest path. If the width of the river is 156m.

A.$1\text{ second}$
B.$\dfrac{13}{12}\text{ seconds}$
C.$\dfrac{\sqrt{3}}{2}\text{ seconds}$
D.$\sqrt{3}\text{ seconds}$

Answer 1

Hint: The shortest distance is the perpendicular distance (AB) of 156m. The shortest time will be taken if the boat travels with its velocity in still water. So, we have to find the time taken to travel the shortest distance and the time taken to cross the river at the least time and take the difference between them.

Complete step by step answer:

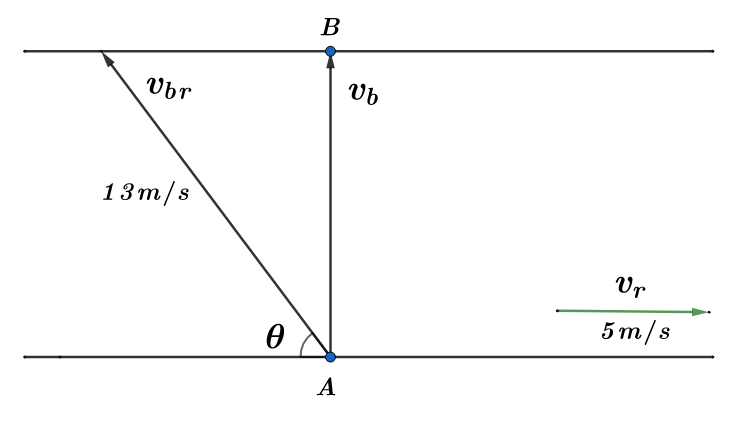
So, the shortest distance is the distance AB, which is the perpendicular distance between the banks of the river. In order to keep a straight path from A to B, the horizontal component of the velocity of the boat w.r.t the river $\left( {{v}_{br}} \right)$ should be equal and opposite to the velocity of the river $\left( {{v}_{r}} \right)$. From the figure above ${{v}_{bm}}\cos \theta $ is the horizontal component of ${{v}_{br}}$.

${{v}_{br}}\cos \theta ={{v}_{r}}$
$\Rightarrow 13\cos \theta =5$
$\therefore \cos \theta =\dfrac{5}{13}$ ……. Equation (1)

So, the velocity of the boat w.r.t to the ground is the vertical component of the velocity of the boat w.r.t the river.

${{v}_{m}}={{v}_{br}}\sin \theta $

From equation (1), we can find the value of $\sin \theta $ from the relation ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$.

${{v}_{m}}={{v}_{br}}\left( \dfrac{12}{13} \right)=13\text{ m/s}\times \left( \dfrac{12}{13} \right)$
$\therefore {{v}_{m}}=12\text{ m/s}$

So, the time taken to the distance AB is,

${{t}_{1}}=\dfrac{AB}{{{v}_{m}}}=\dfrac{156m}{12m/s}$
$\therefore {{t}_{1}}=13\text{ seconds}$

To travel the distance with least time, the velocity should be equal to the velocity of the boat w.r.t to the river $\left( {{v}_{br}} \right)$. So, the time taken is,

${{t}_{2}}=\dfrac{d}{{{v}_{br}}}=\dfrac{156m}{13m/s}$
\[\therefore {{t}_{2}}=12\text{ seconds}\]

So the difference between the two times taken is, $T={{t}_{1}}-{{t}_{2}}$, $\therefore T=1\text{ second}$.

So, the answer to the question is option (A).

Note:
Relative velocity is the velocity of an object or a person in another person’s rest frame. In one dimensional condition, it is the difference between the velocities of the two bodies. While in a higher dimension like in 2D and 3D the velocities of the objects are split into components along various axes and the relative velocity is found about each axis.
It can be used in the relativistic case, where the velocities are very small compared to the velocity of light. Galilean transformation is the principle used in these cases.
In an accelerated frame of reference, when a frame of reference is accelerated with respect to the other, the Galilean transformation does not hold.
In special relativity (non-relativistic case), the Galilean transformation is replaced by the Lorentz transformation.