Question

Vector $ \overrightarrow Q $ ​ has a magnitude of $ 8 $ is added to the vector $ \overrightarrow P $ which lies along the X-axis. The resultant of these two vectors is a third vector $ \overrightarrow R $ which lies along the Y-axis and has a magnitude twice that of $ \overrightarrow P $ . The magnitude of $ \overrightarrow P $ is:
(A) $ \dfrac{6}{{\sqrt 5 }} $
(B) $ \dfrac{8}{{\sqrt 5 }} $
(C) $ \dfrac{{12}}{{\sqrt 5 }} $
(D) $ \dfrac{{16}}{{\sqrt 5 }} $

Answer 1

Hint: Vector $ \overrightarrow P $ is along the x-axis and vector $ \overrightarrow R $ is along the y-axis. So they make an angle of $ {90^ \circ } $ with each other. Use this to find the relation between vector $ \overrightarrow P $ and angle between vector $ \overrightarrow Q $ and vector $ \overrightarrow P $ . Then use the formula to find the resultant of two vectors, we will get our required magnitude of the vector $ \overrightarrow P $

Complete Step By Step Answer:

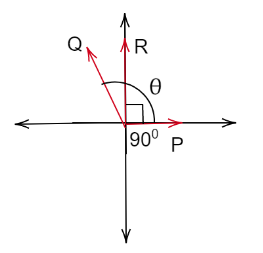
We have been given that the magnitude of the vector $ \overrightarrow Q = 8 $
We can see from the above graph vector $ \overrightarrow R $ is perpendicular to the vector $ \overrightarrow P $
For finding the relation between vector $ \overrightarrow Q $ and vector $ \overrightarrow P $
 $ \tan {90^ \circ } = \dfrac{{Q\sin \theta }}{{P + Q\cos \theta }} $
Putting the value of the vector $ \overrightarrow Q $
 $ \Rightarrow \tan {90^ \circ } = \dfrac{{8\sin \theta }}{{P + 8\cos \theta }} $
 $ \because \tan {90^ \circ } = \infty $
 $ \Rightarrow P + 8\cos \theta = 0 $
 $ \Rightarrow \cos \theta = \dfrac{{ - P}}{8} $
Now finding the resultant to get the relation between all three vectors,
 $ \left| {\overrightarrow R } \right| = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } $
Above is the equation for the product of two vectors, where $ \overrightarrow P $ and $ \overrightarrow Q $ are the magnitudes of the vectors and $ \theta $ is the angle between them.
We have been given vector $ \overrightarrow R $ is twice of vector $ \overrightarrow P $
Putting the values of vector $ \overrightarrow R $ and $ \cos \theta $ in the above equation
 $ \Rightarrow \left( {2P} \right) = \sqrt {{P^2} + {8^2} + 2P(8)\left( {\dfrac{{ - P}}{8}} \right)} $
 $ \Rightarrow {(2P)^2} = {P^2} + {8^2} - 2{P^2} $
 $ \Rightarrow 5{P^2} = 64 $
 $ \Rightarrow P = \sqrt {\dfrac{{64}}{5}} $
 $ \Rightarrow P = \dfrac{8}{{\sqrt 5 }} $
Therefore the magnitude of the vector $ \overrightarrow P $ is found to be $ \dfrac{8}{{\sqrt 5 }} $
Hence, option B) $ \dfrac{8}{{\sqrt 5 }} $ is the correct option.

Note:
The length of the vector is known as the magnitude of the vector. The resultant of any two vectors is equal to the vector sum of those two vectors. For $ \tan {90^ \circ } = \infty $ the denominator has to be zero that is why we got $ P + 8\cos \theta = 0 $ .