
Vapour pressure of pure acetone and chloroform at $328\,K$ are $741.8mmHg$ and $632.8mmHg$ respectively. Assuming that they form an ideal solution over the entire range of composition. Plot ${P_{total}},{P_{chloroform}}$ and ${P_{acetone}}$ as function of \[{X_{acetone}}.\] the experiment data observed for different compositions of mixture is,
${X_{acetone}}$ $0$ $11.8$ $23.4$ $36.0$ $50.8$ $58.2$ $64.5$ $72.1$ ${P_{acetone}}\,\left( {mm/Hg} \right)$ $0$ $54.9$ $110.1$ $202.4$ $322.7$ $405.9$ $454.1$ $521.1$ ${P_{chloroform}}\left( {mm/Hg} \right)$ \[632.8\] $548.1$ $469.4$ $359.7$ \[257.7\] $193.6$ $161.2$ $120.7$
Plot this data also on the same graph paper. Indicate whether it has positive deviation or negative deviation from the ideal solution.
| ${X_{acetone}}$ | $0$ | $11.8$ | $23.4$ | $36.0$ | $50.8$ | $58.2$ | $64.5$ | $72.1$ |
| ${P_{acetone}}\,\left( {mm/Hg} \right)$ | $0$ | $54.9$ | $110.1$ | $202.4$ | $322.7$ | $405.9$ | $454.1$ | $521.1$ |
| ${P_{chloroform}}\left( {mm/Hg} \right)$ | \[632.8\] | $548.1$ | $469.4$ | $359.7$ | \[257.7\] | $193.6$ | $161.2$ | $120.7$ |
Answer
586.2k+ views
Hint:We have to know about Raoult’s law in order to solve this question. Raoult’s law conveys the vapour pressure of the solvent to mole fraction times the vapour pressure of the pure solvent. We can plot the graph and find the ${P_{total}}$ by plotting the sum of ${P_{acetone}}$ and ${P_{chloroform}}$ to the mole fraction of acetone $\left( {{X_{acetone}}} \right).$ from the plot, we can determine the type of deviation for the solution.
Complete step by step answer:
Now let us discuss Raoult's law and mole fraction.
The equilibrium between a liquid and its vapour produces a characteristic vapour pressure for each substance that depends on the temperature. The lowering of the vapour pressure is caused by a lesser ability of the solvent to evaporate, so equilibrium is reached with a smaller concentration of the solvent in the gas phase. The vapour pressure of a solution is expressed using Raoult’s law:
${{\text{P}}_{{\text{solv}}}}{\text{ = }}{{\text{X}}_{{\text{solv}}}}{{\text{P}}^{\text{o}}}_{{\text{solv}}}$
The vapour pressure of the solvent $\left( {{{\text{P}}_{{\text{solv}}}}} \right)$ above a dilute solution is equal to the mole fraction of the solvent ${\text{(}}{{\text{X}}_{{\text{solv}}}}{\text{)}}$ times the vapour pressure of the pure solvent $\left( {{{\text{P}}^{\text{o}}}_{{\text{solv}}}} \right).$
We can define mole fraction of a substance in a solution as the number of moles of that substance divided by the total number of moles of all substances present. The formula is,
$
{X_{\text{A}}}{\text{ = }}\dfrac{{Moles\,of\,A{\text{ }}(in\,mol)}}{{Moles\,of\,A{\text{ }}(in{\text{ }}mol){\text{ }} + Moles\,of\,B{\text{ }}(in{\text{ }}mol){\text{ }} + Moles\,of\,C{\text{ }}(in{\text{ }}mol){\text{ }} + ...}} \\
\\
\\
$
${X_{\text{A}}} = \dfrac{{Moles\,of\,A{\text{ }}(in\,mol)}}{{Total\,number\,of\,moles\,of\,components\,(in\,mol)}}$
We can calculate the total vapour pressure by summing the vapour pressures of acetone and chloroform. The table below shows us the sum of two vapour pressures,
Let us draw a plot now taking the total vapour pressure on the y-axis and mole fraction of acetone in the x-axis.
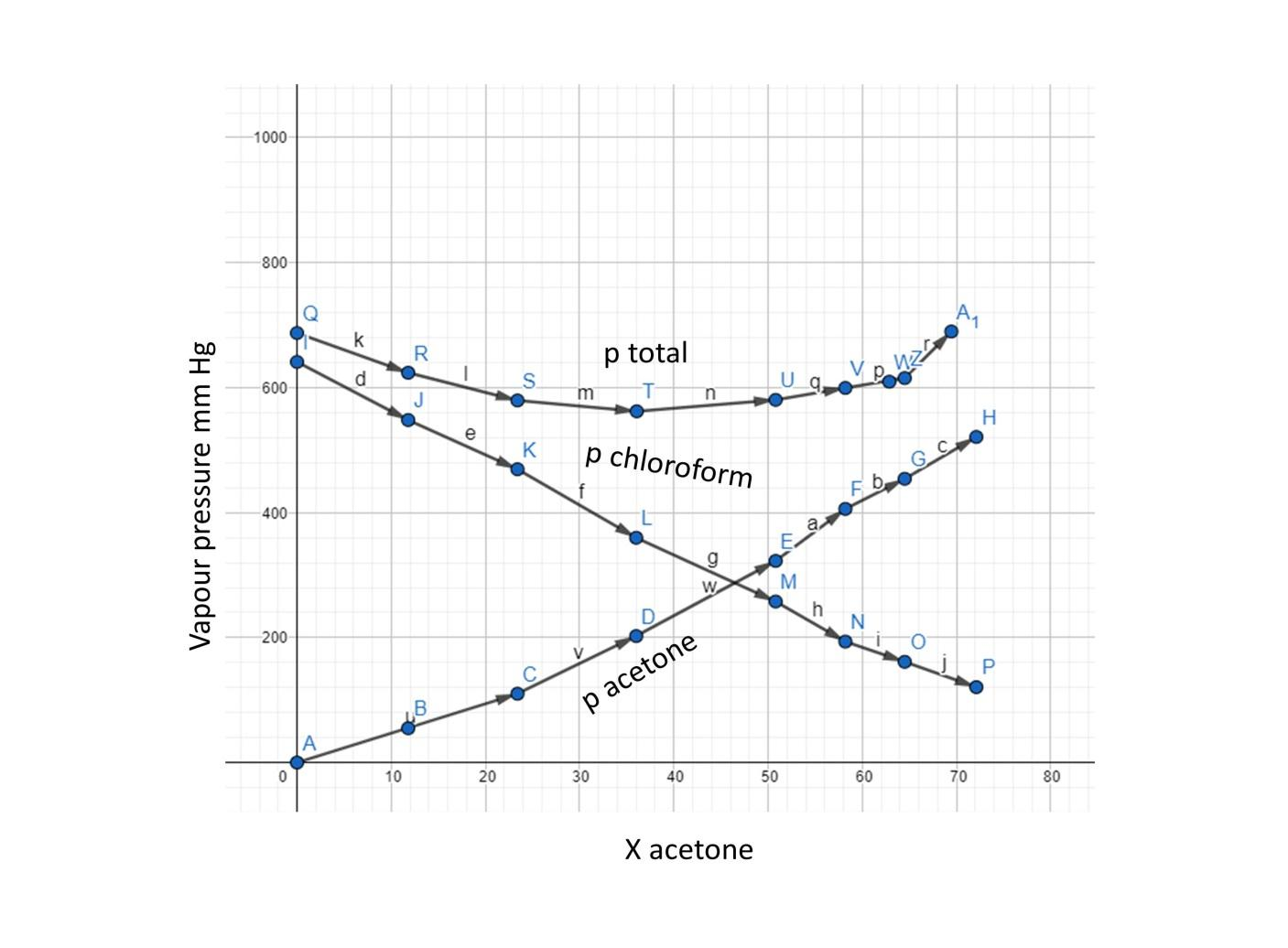
We can see from the above plot that the curve of total vapour pressure is downwards so it’s negative deviation from the ideal solution.
We can see a negative deviation from Raoult’s law when the intermolecular forces between the dissimilar molecules are stronger than the average of the intermolecular forces in the pure substances.
Note:
We can see a positive deviation from Raoult’s law when the observed vapour pressure is greater than expected and it occurs when the A-B attractions are weaker than the average of the attractions in the pure components of the mixture.
Complete step by step answer:
Now let us discuss Raoult's law and mole fraction.
The equilibrium between a liquid and its vapour produces a characteristic vapour pressure for each substance that depends on the temperature. The lowering of the vapour pressure is caused by a lesser ability of the solvent to evaporate, so equilibrium is reached with a smaller concentration of the solvent in the gas phase. The vapour pressure of a solution is expressed using Raoult’s law:
${{\text{P}}_{{\text{solv}}}}{\text{ = }}{{\text{X}}_{{\text{solv}}}}{{\text{P}}^{\text{o}}}_{{\text{solv}}}$
The vapour pressure of the solvent $\left( {{{\text{P}}_{{\text{solv}}}}} \right)$ above a dilute solution is equal to the mole fraction of the solvent ${\text{(}}{{\text{X}}_{{\text{solv}}}}{\text{)}}$ times the vapour pressure of the pure solvent $\left( {{{\text{P}}^{\text{o}}}_{{\text{solv}}}} \right).$
We can define mole fraction of a substance in a solution as the number of moles of that substance divided by the total number of moles of all substances present. The formula is,
$
{X_{\text{A}}}{\text{ = }}\dfrac{{Moles\,of\,A{\text{ }}(in\,mol)}}{{Moles\,of\,A{\text{ }}(in{\text{ }}mol){\text{ }} + Moles\,of\,B{\text{ }}(in{\text{ }}mol){\text{ }} + Moles\,of\,C{\text{ }}(in{\text{ }}mol){\text{ }} + ...}} \\
\\
\\
$
${X_{\text{A}}} = \dfrac{{Moles\,of\,A{\text{ }}(in\,mol)}}{{Total\,number\,of\,moles\,of\,components\,(in\,mol)}}$
We can calculate the total vapour pressure by summing the vapour pressures of acetone and chloroform. The table below shows us the sum of two vapour pressures,
| ${X_{acetone}}$ | $0$ | $11.8$ | $23.4$ | $36.0$ | $50.8$ | $58.2$ | $64.5$ | $72.1$ |
| ${P_{acetone}}\,\left( {mm/Hg} \right)$ | $0$ | $54.9$ | $110.1$ | $202.4$ | $322.7$ | $405.9$ | $454.1$ | $521.1$ |
| ${P_{chloroform}}\left( {mm/Hg} \right)$ | \[632.8\] | $548.1$ | $469.4$ | $359.7$ | \[257.7\] | $193.6$ | $161.2$ | $120.7$ |
| ${P_{total}}\left( {mm/Hg} \right)$ | $623.8$ | $603.0$ | $579.5$ | $562.1$ | $580.4$ | $599.5$ | $615.3$ | ${\text{641}}{\text{.8}}$ |
Let us draw a plot now taking the total vapour pressure on the y-axis and mole fraction of acetone in the x-axis.

We can see from the above plot that the curve of total vapour pressure is downwards so it’s negative deviation from the ideal solution.
We can see a negative deviation from Raoult’s law when the intermolecular forces between the dissimilar molecules are stronger than the average of the intermolecular forces in the pure substances.
Note:
We can see a positive deviation from Raoult’s law when the observed vapour pressure is greater than expected and it occurs when the A-B attractions are weaker than the average of the attractions in the pure components of the mixture.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




