Question

What is the value of x in a triangle with angles 70, 60 and $8x+2$ ?

Answer 1

Hint: To find the value of x, we will use the triangle angle-sum theorem which states that the sum of interiors angles of a triangle is equal to $180{}^\circ $ . We will then get an equation and we have to solve for x.

Complete step-by-step solution:
We have to find the value of x in a triangle with angles 70, 60 and $8x+2$ . We know that triangle angle-sum theorem states that the sum of interior angles of a triangle is equal to $180{}^\circ $.

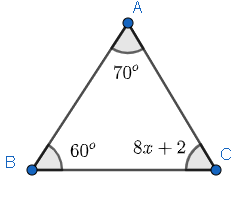
Therefore, we can write the sum of the given angles as $180{}^\circ $ .
$\Rightarrow 70{}^\circ +60{}^\circ +\left( 8x+2 \right)=180{}^\circ $
We have obtained an equation. We need to find the value of x. Let us first add the constants in the LHS.
$\Rightarrow 132{}^\circ +8x=180{}^\circ $
Now, we have to collect all the constants in the RHS. Let us move $132{}^\circ $ to the RHS.
$\Rightarrow 8x=180{}^\circ -132{}^\circ $
Now, let us subtract 132 from 180.
$\Rightarrow 8x=48{}^\circ $
Now, we have to move the coefficient of x from the LHS to the RHS.
$\Rightarrow x=\dfrac{48{}^\circ }{8}$
Let us divide 48 by 8.
$\Rightarrow x=6{}^\circ $
Hence, the value of x is 6.

Note: Students must know the triangle angle-sum theorem. There are many properties associated with a triangle. They must know how to solve an algebraic equation. When a positive term is moved from one side to another, it will become negative. Similarly, when a negative term is moved from one side to another, it will become positive. When a multiplier or multiplicand is moved from one side to the other, it will be the divisor. Similarly, when a divisor is moved in a similar manner, it will form a product.