
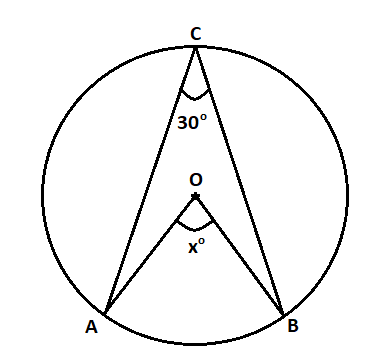
What is the value of $x$ from the given figure?

Answer
489.9k+ views
Hint: Here we are asked to find the angle \[x^\circ \] from the given figure. As we can see that the angles $\angle ACB$ and the angle $\angle AOB = x^\circ $ are both subtended by the same sector of the circle. To find the measure of the angle $\angle AOB = x^\circ $ we will use the property of the circle concerning angles. That is, the angle subtended from a sector to the center of the circle is twice the angle subtended from the same sector to any other point on the circle.
Complete step-by-step answer:
We aim to find the measure of the angle \[x^\circ \] from the given figure.
Let us observe the diagram. We are given the measure of one angle is $\angle ACB = 30^\circ $ which is subtended from a sector of a circle to a point $C$ on the circle. And we are asked to find the measure of the angle $\angle AOB = x^\circ $ that is subtended from the same sector to the center of the circle.
From the properties of the circle, we have the angle subtended from a sector of a circle is twice the angle subtended from the same sector to any other point on the remaining part of the sector.
So, from the given diagram we get \[\angle AOB = 2\angle ACB\]
Now let us apply the measures of these angles.
\[ \Rightarrow x^\circ = 2 \times 30^\circ \]
On simplifying this we get
$ \Rightarrow x^\circ = 60^\circ $
Thus, we got the measure of the angle $x^\circ $ that is $\angle AOB = 60^\circ $.
Hence, the value of $x$ is $60$ .
Note: A sector of a circle is nothing but the part of a circle formed by two radii of that circle. In this problem, the two radii are $OA$ and $OB$ . The shape of the sector is more or less like a piece of pizza. The sector will divide the circle into two parts- the small part is known as the minor sector and the large part is known as the major sector.
Complete step-by-step answer:
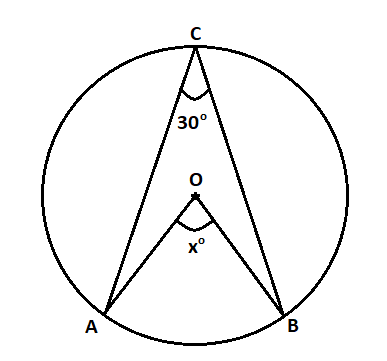
We aim to find the measure of the angle \[x^\circ \] from the given figure.

Let us observe the diagram. We are given the measure of one angle is $\angle ACB = 30^\circ $ which is subtended from a sector of a circle to a point $C$ on the circle. And we are asked to find the measure of the angle $\angle AOB = x^\circ $ that is subtended from the same sector to the center of the circle.
From the properties of the circle, we have the angle subtended from a sector of a circle is twice the angle subtended from the same sector to any other point on the remaining part of the sector.
So, from the given diagram we get \[\angle AOB = 2\angle ACB\]
Now let us apply the measures of these angles.
\[ \Rightarrow x^\circ = 2 \times 30^\circ \]
On simplifying this we get
$ \Rightarrow x^\circ = 60^\circ $
Thus, we got the measure of the angle $x^\circ $ that is $\angle AOB = 60^\circ $.
Hence, the value of $x$ is $60$ .
Note: A sector of a circle is nothing but the part of a circle formed by two radii of that circle. In this problem, the two radii are $OA$ and $OB$ . The shape of the sector is more or less like a piece of pizza. The sector will divide the circle into two parts- the small part is known as the minor sector and the large part is known as the major sector.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




